2 3 X 3 2
straightsci
Aug 28, 2025 · 6 min read
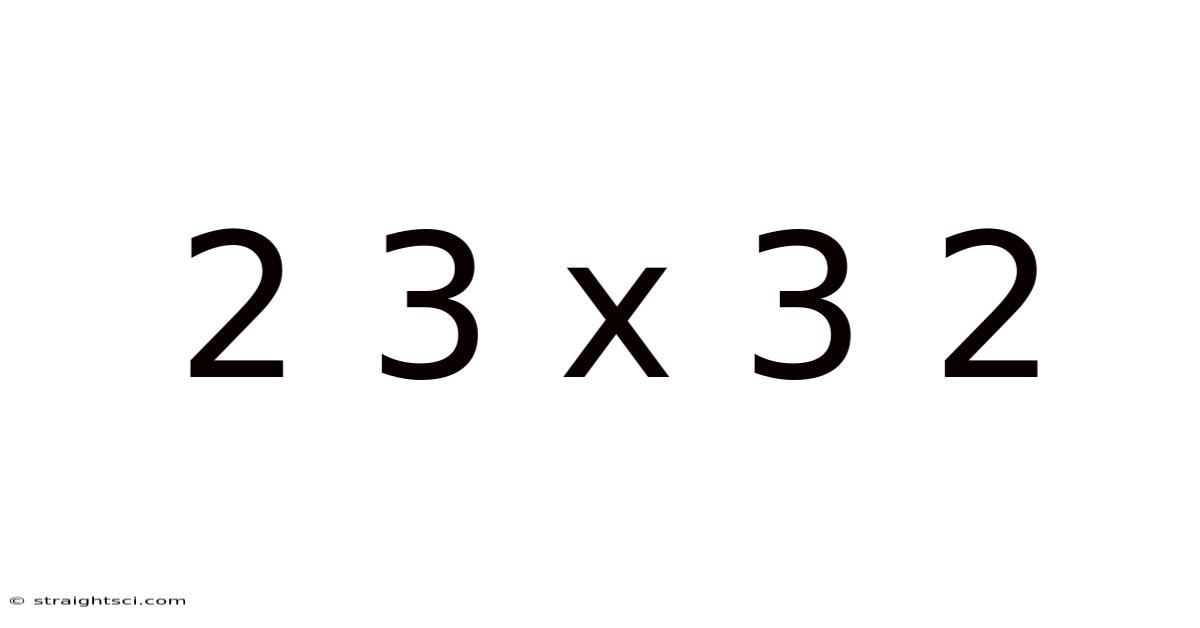
Table of Contents
Decoding 2 x 3 x 3 x 2: A Deep Dive into Matrix Multiplication and its Applications
This article delves into the mathematical concept of matrix multiplication, specifically focusing on a 2 x 3 matrix multiplied by a 3 x 2 matrix. We'll explore the mechanics of the calculation, the underlying principles, and the wide range of applications this seemingly simple operation has in diverse fields. Understanding matrix multiplication is crucial for anyone studying linear algebra, computer science, engineering, or physics.
Introduction: Understanding Matrices and Matrix Multiplication
A matrix is a rectangular array of numbers, symbols, or expressions, arranged in rows and columns. The dimensions of a matrix are described as m x n, where 'm' represents the number of rows and 'n' represents the number of columns. For example, a 2 x 3 matrix has two rows and three columns.
Matrix multiplication isn't simply multiplying corresponding elements like in scalar multiplication. It's a more complex operation that follows specific rules. To multiply two matrices, the number of columns in the first matrix must equal the number of rows in the second matrix. The resulting matrix will have the number of rows of the first matrix and the number of columns of the second matrix. In our case, a 2 x 3 matrix multiplied by a 3 x 2 matrix will result in a 2 x 2 matrix.
The Mechanics of Multiplying a 2 x 3 Matrix by a 3 x 2 Matrix
Let's represent our matrices as follows:
Matrix A (2 x 3):
[ a11 a12 a13 ]
[ a21 a22 a23 ]
Matrix B (3 x 2):
[ b11 b12 ]
[ b21 b22 ]
[ b31 b32 ]
To calculate the resulting 2 x 2 matrix (let's call it C), we perform the following multiplications and additions:
- Element C11: (a11 * b11) + (a12 * b21) + (a13 * b31)
- Element C12: (a11 * b12) + (a12 * b22) + (a13 * b32)
- Element C21: (a21 * b11) + (a22 * b21) + (a23 * b31)
- Element C22: (a21 * b12) + (a22 * b22) + (a23 * b32)
Matrix C (2 x 2):
[ C11 C12 ]
[ C21 C22 ]
Each element in the resulting matrix C is the dot product of a row from matrix A and a column from matrix B. This is a fundamental concept in linear algebra. Let's illustrate with a numerical example:
Example:
Let's say:
Matrix A:
[ 1 2 3 ]
[ 4 5 6 ]
Matrix B:
[ 7 8 ]
[ 9 10]
[ 11 12]
Now, let's calculate the elements of matrix C:
- C11: (1 * 7) + (2 * 9) + (3 * 11) = 7 + 18 + 33 = 58
- C12: (1 * 8) + (2 * 10) + (3 * 12) = 8 + 20 + 36 = 64
- C21: (4 * 7) + (5 * 9) + (6 * 11) = 28 + 45 + 66 = 139
- C22: (4 * 8) + (5 * 10) + (6 * 12) = 32 + 50 + 72 = 154
Therefore, the resulting matrix C is:
Matrix C:
[ 58 64 ]
[ 139 154 ]
Mathematical Properties of Matrix Multiplication
Matrix multiplication possesses several important properties:
-
Associativity: (A x B) x C = A x (B x C). This means the order of multiplication doesn't affect the result, provided the dimensions allow for the multiplication.
-
Distributivity: A x (B + C) = (A x B) + (A x C). This property applies to matrix addition and multiplication.
-
Non-Commutativity: Generally, A x B ≠ B x A. The order of multiplication significantly matters. While A x B might be possible, B x A might not be defined due to incompatible dimensions, or even if defined, the resulting matrices will be different.
-
Identity Matrix: There exists an identity matrix, denoted by I, such that A x I = I x A = A. The identity matrix is a square matrix with 1s on the main diagonal and 0s elsewhere.
-
Zero Matrix: Multiplying any matrix by a zero matrix (a matrix with all elements equal to zero) results in a zero matrix.
Applications of 2 x 3 x 3 x 2 Matrix Multiplication and its Generalizations
The seemingly specific case of multiplying a 2 x 3 matrix by a 3 x 2 matrix is actually a fundamental building block in numerous applications. Let's explore some examples where matrix multiplication, and its generalizations to larger matrices, play a crucial role:
-
Linear Transformations: Matrices can represent linear transformations in space. Multiplying a matrix by a vector (a column matrix) applies the transformation to that vector. The 2 x 3 and 3 x 2 matrices could represent transformations between 3-dimensional and 2-dimensional spaces. For example, projecting a 3D object onto a 2D plane involves such matrix multiplication.
-
Computer Graphics: Matrix multiplication is the backbone of computer graphics. Transformations like rotation, scaling, and translation of objects are efficiently represented and applied using matrices. Complex animations rely heavily on these matrix operations.
-
Image Processing: Image manipulation, such as filtering, edge detection, and image enhancement, often involves matrix operations. Convolutional neural networks, widely used in image recognition, extensively use matrix multiplication.
-
Machine Learning: Machine learning algorithms, particularly those dealing with large datasets, use matrix operations at their core. Calculations involving weights and biases in neural networks, and operations in support vector machines, heavily rely on efficient matrix multiplications.
-
Data Analysis and Statistics: Statistical analysis often uses matrices to represent datasets and perform operations such as correlation analysis, principal component analysis (PCA), and regression analysis.
-
Physics and Engineering: Matrices are ubiquitous in physics and engineering. They are used to solve systems of linear equations that model physical phenomena, such as in structural analysis, circuit analysis, and fluid dynamics. Quantum mechanics relies on matrix mechanics to represent quantum states and operators.
Computational Considerations and Efficiency
Performing matrix multiplication can be computationally intensive, especially for large matrices. The naive approach of directly applying the formula has a time complexity of O(n³), where 'n' is the dimension of the matrices. However, efficient algorithms, such as Strassen's algorithm, can reduce the time complexity to O(n^log₂7), which is significantly faster for very large matrices.
Optimized libraries and hardware, such as GPUs, are commonly used to accelerate matrix multiplications. These optimizations are crucial for applications like machine learning and computer graphics that involve billions of matrix calculations.
Frequently Asked Questions (FAQ)
-
Q: What happens if the number of columns in the first matrix doesn't match the number of rows in the second matrix?
- A: Matrix multiplication is not defined in this case. The operation cannot be performed.
-
Q: Is matrix multiplication commutative?
- A: No, matrix multiplication is generally not commutative. A x B ≠ B x A, except in special cases.
-
Q: What are some real-world examples of matrix multiplication beyond those mentioned?
- A: Applications extend to cryptography, economics (input-output models), and network analysis.
-
Q: Are there different types of matrix multiplications?
- A: While standard matrix multiplication is the most common, other forms exist, such as Hadamard product (element-wise multiplication) and Kronecker product.
-
Q: How can I learn more about matrix multiplication and linear algebra?
- A: Numerous textbooks and online courses are available, catering to various levels of mathematical expertise.
Conclusion: The Significance of 2 x 3 x 3 x 2 and Beyond
The seemingly simple operation of multiplying a 2 x 3 matrix by a 3 x 2 matrix underpins a vast array of critical applications in various scientific and technological fields. Understanding the mechanics, mathematical properties, and computational aspects of matrix multiplication is not only essential for mastering linear algebra but also for appreciating its power and versatility in modern computing and scientific modeling. This seemingly simple mathematical concept forms the foundation for many of the technological advancements we see around us, highlighting its enduring importance. The journey from understanding the basic operations to appreciating its broader implications is a rewarding one for any aspiring scientist, engineer, or computer scientist.
Latest Posts
Latest Posts
-
Copper Reaction With Silver Nitrate
Aug 28, 2025
-
Comma In Front Of Because
Aug 28, 2025
-
Is Snow Liquid Or Solid
Aug 28, 2025
-
Effects Of The Hiroshima Bombing
Aug 28, 2025
-
What Are Length And Width
Aug 28, 2025
Related Post
Thank you for visiting our website which covers about 2 3 X 3 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.