2 3 X 2 3
straightsci
Sep 23, 2025 · 5 min read
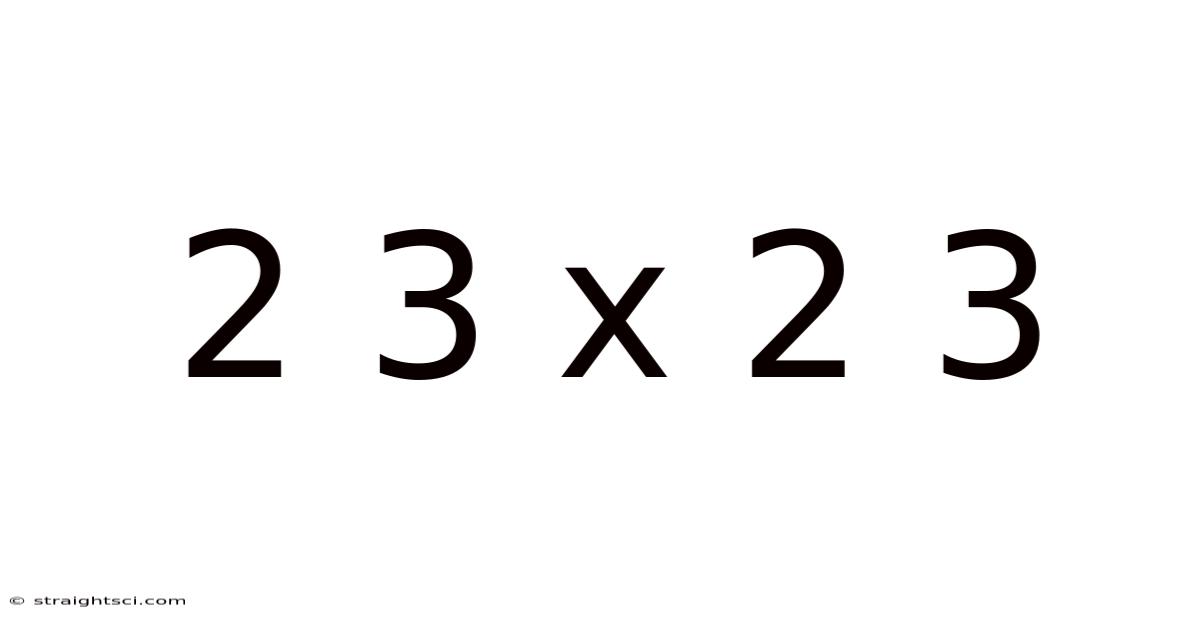
Table of Contents
Decoding 2³ x 2³: Exploring Exponents, Multiplication, and Volume
This article delves into the seemingly simple mathematical expression 2³ x 2³, unraveling its meaning and demonstrating its applications beyond basic arithmetic. We'll explore the concept of exponents, the rules of multiplication, and how this specific expression relates to practical scenarios, particularly in understanding volume calculations. This comprehensive guide is designed for anyone, from those brushing up on basic math to those wanting a deeper understanding of exponential functions.
Introduction: Understanding the Fundamentals
The expression 2³ x 2³ involves two key mathematical concepts: exponents and multiplication. Let's break down each component before tackling the overall expression.
-
Exponents (Indices): An exponent, also known as a power or index, indicates how many times a number (the base) is multiplied by itself. In 2³, the base is 2 and the exponent is 3. This means 2³ = 2 x 2 x 2 = 8. The exponent tells us to perform repeated multiplication.
-
Multiplication: This is a fundamental arithmetic operation representing the repeated addition of a number. In the context of 2³ x 2³, we are multiplying the result of 2³ by itself.
Step-by-Step Calculation of 2³ x 2³
-
Calculate 2³: As explained above, 2³ means 2 multiplied by itself three times: 2 x 2 x 2 = 8.
-
Rewrite the Expression: Now we can rewrite the original expression: 2³ x 2³ = 8 x 8.
-
Perform the Multiplication: Multiplying 8 by 8 gives us the final answer: 8 x 8 = 64.
Therefore, 2³ x 2³ = 64.
Exploring Alternative Approaches: Laws of Exponents
While the step-by-step method is straightforward, understanding the laws of exponents provides a more efficient approach, especially for more complex expressions. One crucial law is the rule for multiplying numbers with the same base:
- Rule: aᵐ x aⁿ = aᵐ⁺ⁿ
This rule states that when multiplying two numbers with the same base (a), you can add their exponents (m and n).
Applying this to our expression:
2³ x 2³ = 2⁽³⁺³⁾ = 2⁶
Now, calculating 2⁶: 2 x 2 x 2 x 2 x 2 x 2 = 64. We arrive at the same answer, but this method is quicker and more adaptable for more intricate problems.
Real-World Applications: Volume Calculations
Understanding 2³ x 2³ has practical applications, particularly in calculating volumes. Imagine a cube with sides of length 2 units (e.g., 2 centimeters, 2 meters, or 2 inches).
- Volume of a Cube: The volume of a cube is calculated by multiplying its length, width, and height. Since all sides of a cube are equal, the volume is side x side x side, or side³.
In our case, with a side length of 2 units:
Volume = 2³ = 8 cubic units.
Now, imagine we have eight such cubes arranged to form a larger cube. This larger cube would have dimensions of 2 x 2 x 2 units. The total volume of this larger cube is:
Volume = 2 x 2 x 2 x 2 x 2 x 2 = 2⁶ = 64 cubic units.
Alternatively, we could consider this as the volume of eight individual cubes, each with a volume of 8 cubic units:
Total Volume = 8 cubes x 8 cubic units/cube = 64 cubic units.
This perfectly illustrates the expression 2³ x 2³ = 64. The result represents the volume of a larger cube composed of eight smaller cubes.
Expanding the Concept: Beyond Cubes and 2³ x 2³
The principles demonstrated here extend far beyond the specific example of 2³ x 2³. Understanding exponents and their rules allows us to tackle a wide range of problems involving:
-
Geometric Calculations: Calculating the volume of various three-dimensional shapes, including rectangular prisms, cylinders, and spheres, often involves exponential expressions.
-
Scientific Notation: Exponents are essential in representing very large or very small numbers in science. This is particularly important in fields such as physics, chemistry, and astronomy.
-
Compound Interest: In finance, compound interest calculations heavily rely on exponential functions. Understanding how exponents affect growth is crucial for comprehending investment strategies.
-
Computer Science: Binary numbers (base-2) utilize exponential notation. Understanding this is critical in digital systems and computer programming.
Frequently Asked Questions (FAQ)
-
Q: What is the difference between 2³ + 2³ and 2³ x 2³?
-
A: 2³ + 2³ involves addition; you add the results of 2³ (which is 8) to itself: 8 + 8 = 16. 2³ x 2³ involves multiplication; you multiply the results of 2³ (which is 8) by itself: 8 x 8 = 64. Addition and multiplication produce vastly different results.
-
Q: Can I apply the exponent rule (aᵐ x aⁿ = aᵐ⁺ⁿ) to expressions with different bases?
-
A: No, this rule only applies when the bases are identical. For example, you cannot simplify 2³ x 3² using this rule. You would need to calculate 2³ (which is 8) and 3² (which is 9) and then multiply them: 8 x 9 = 72.
-
Q: What if the exponents were negative?
-
A: Negative exponents represent reciprocals. For instance, 2⁻³ = 1/2³ = 1/8. The rules of exponents still apply, but you need to consider the reciprocal nature of negative exponents.
-
Q: How can I solve more complex exponential expressions?
-
A: Mastering the basic laws of exponents (such as the rule for multiplication, division, and raising a power to a power) is key. Practice with various examples is crucial to build proficiency. Understanding the order of operations (PEMDAS/BODMAS) is also essential.
Conclusion: A Foundation for Further Learning
The seemingly simple expression 2³ x 2³ provides a gateway to understanding fundamental mathematical concepts. From mastering exponents and multiplication to appreciating the practical applications in volume calculations and beyond, this exploration forms a solid foundation for tackling more complex mathematical challenges. Remember that consistent practice and a thorough understanding of the underlying principles are key to success in mathematics. By breaking down complex problems into smaller, manageable steps, and by leveraging the rules of exponents, you can unlock a deeper appreciation for the power and elegance of mathematics.
Latest Posts
Latest Posts
-
Units Of Measure Kinetic Energy
Sep 24, 2025
-
Convert 5 Pounds Into Kilograms
Sep 24, 2025
-
Fall Arrest Vs Fall Restraint
Sep 24, 2025
-
Range Of A Projectile Equation
Sep 24, 2025
-
128 Over 79 Blood Pressure
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about 2 3 X 2 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.