2/3 Times 2/3 Times 2/3
straightsci
Sep 21, 2025 · 5 min read
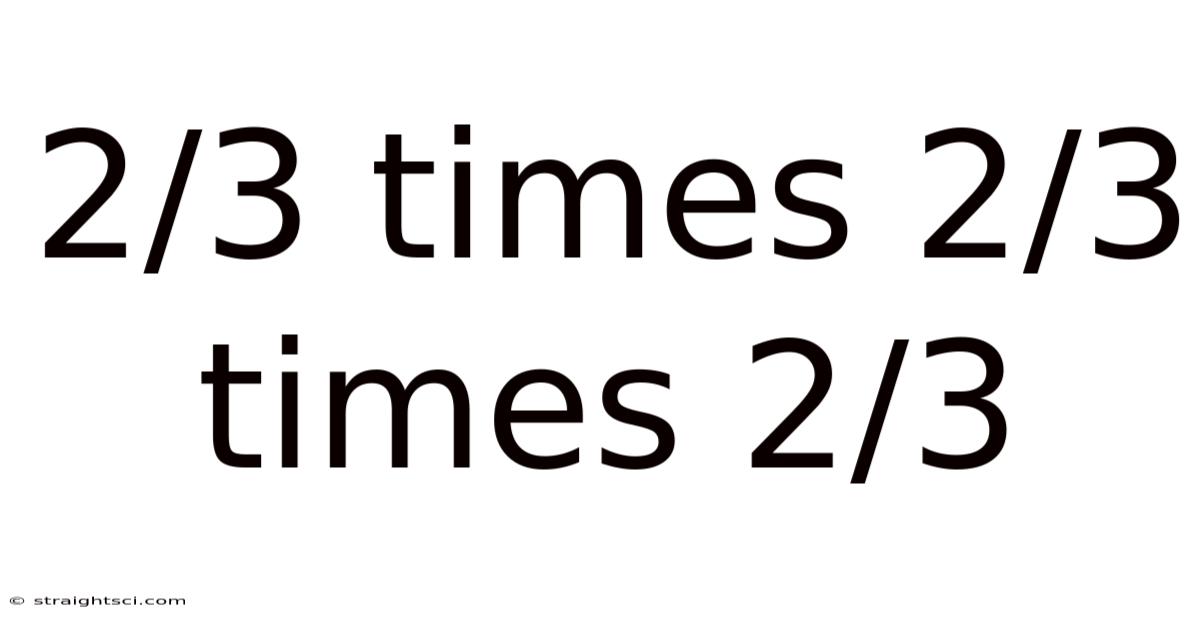
Table of Contents
Unraveling the Mystery: 2/3 x 2/3 x 2/3 and the Power of Repeated Multiplication
What happens when you multiply a fraction by itself repeatedly? This seemingly simple question, represented by the expression 2/3 x 2/3 x 2/3, opens a door to a fascinating exploration of fractions, exponents, and their practical applications. This article will delve deep into understanding this specific calculation, explore its underlying mathematical principles, and demonstrate its relevance in various real-world scenarios. We'll also tackle frequently asked questions and provide a solid foundation for anyone looking to improve their understanding of fractional mathematics.
Understanding the Basics: Multiplying Fractions
Before we tackle the core problem of 2/3 x 2/3 x 2/3, let's refresh our understanding of multiplying fractions. The process is straightforward:
- Multiply the numerators: The numerators are the top numbers in the fractions. In our case, these are all 2.
- Multiply the denominators: The denominators are the bottom numbers in the fractions. In our example, these are all 3.
- Simplify the resulting fraction: Once you've multiplied the numerators and denominators, simplify the resulting fraction to its lowest terms.
For example, if we were multiplying 1/2 by 1/4, we would:
- Multiply the numerators: 1 x 1 = 1
- Multiply the denominators: 2 x 4 = 8
- Simplify the resulting fraction: The fraction 1/8 is already in its simplest form.
Solving 2/3 x 2/3 x 2/3
Now, let's apply this knowledge to our problem: 2/3 x 2/3 x 2/3.
- Multiply the numerators: 2 x 2 x 2 = 8
- Multiply the denominators: 3 x 3 x 3 = 27
- Simplify the resulting fraction: The fraction 8/27 is already in its simplest form, as 8 and 27 share no common factors other than 1.
Therefore, 2/3 x 2/3 x 2/3 = 8/27.
Exponents and Repeated Multiplication: A Deeper Dive
Repeated multiplication, as seen in our example, can be expressed more concisely using exponents. An exponent indicates how many times a number (the base) is multiplied by itself. In our case, the base is 2/3, and we are multiplying it by itself three times. This can be written as (2/3)³.
The calculation remains the same: (2/3)³ = (2/3) x (2/3) x (2/3) = 8/27. Understanding exponents is crucial for simplifying more complex calculations involving repeated multiplication of fractions or other numbers.
Visualizing the Problem: A Geometric Approach
Fractions can often be visualized geometrically. Imagine a square with sides of length 1 unit. If we take 2/3 of that square, we're left with a rectangle that occupies 2/3 of the total area.
Now, let's take 2/3 of that rectangle. We're effectively taking 2/3 of 2/3, which is (2/3)² = 4/9 of the original square's area.
Finally, let's take 2/3 of the remaining area. This represents (2/3)³ = 8/27 of the original square's area. This visual representation helps solidify the concept and makes the calculation more intuitive.
Real-World Applications: Where Does This Matter?
While it might seem like an abstract mathematical exercise, understanding repeated multiplication of fractions has practical applications in various fields:
- Probability: Consider a situation where the probability of a successful event is 2/3. If this event occurs three times independently, the probability of all three events succeeding is (2/3)³ = 8/27. This type of calculation is fundamental in probability theory and statistics.
- Compound Interest: While not directly involving fractions in this specific form, the concept of repeated multiplication is crucial in calculating compound interest. The principal amount is multiplied repeatedly over time, leading to exponential growth. Fractions might arise if we consider interest rates as fractions of the principal amount.
- Decay Processes: Just like compound interest involves growth, many natural processes involve decay. For example, the radioactive decay of an element follows an exponential decay model, where the remaining quantity is multiplied by a fraction repeatedly over time.
- Geometric Series: In mathematics, a geometric series is a sum of terms where each term is a constant multiple of the previous term. Understanding repeated multiplication of fractions is key to understanding and manipulating geometric series.
- Engineering and Physics: Repeated multiplication of fractions arises in various engineering and physics applications, for instance, when modeling attenuation of signals or dealing with efficiency losses in systems.
Extending the Concept: Beyond 2/3
The principle we've explored extends beyond the specific fraction 2/3. We can apply the same method to any fraction raised to a power. For example:
- (1/2)³ = 1/8
- (3/4)² = 9/16
- (5/7)⁴ = 625/2401
The key is always to multiply the numerators together and the denominators together, then simplify the resulting fraction.
Frequently Asked Questions (FAQ)
Q: What is the decimal equivalent of 8/27?
A: 8/27 ≈ 0.2963
Q: Can I solve this using a calculator?
A: Yes, most calculators can handle fractional calculations and exponents. Simply enter (2/3)^3 or 2/32/32/3.
Q: Is there a way to estimate the answer without calculating precisely?
A: Yes, you can approximate. Since 2/3 is slightly less than 1, multiplying it by itself repeatedly will result in a value significantly smaller than 1, but larger than 0. The closer the fraction is to 1, the slower its repeated multiplication will decrease.
Q: Why is simplifying the fraction important?
A: Simplifying the fraction ensures that the answer is presented in its most concise and easily understandable form. It also makes further calculations easier if needed.
Conclusion: Mastering Fractional Arithmetic
Understanding the calculation of 2/3 x 2/3 x 2/3 is more than just solving a single mathematical problem. It's about grasping the fundamental principles of fractional multiplication, exponents, and their wide-ranging applications. By mastering these concepts, you build a stronger foundation in mathematics, equipping yourself to tackle more complex problems in various disciplines. The seemingly simple act of multiplying fractions repeatedly opens doors to a deeper appreciation of mathematical concepts and their power in solving real-world challenges. Remember the key steps: multiply the numerators, multiply the denominators, and simplify your final answer. With practice and understanding, you can confidently approach similar problems and appreciate the elegance of mathematical principles.
Latest Posts
Latest Posts
-
Opposite Brown On Color Wheel
Sep 21, 2025
-
Half Moon And Half Sun
Sep 21, 2025
-
How Many Weeks Average Pregnancy
Sep 21, 2025
-
What Does A Physicists Do
Sep 21, 2025
-
Problem Of The Week Waterloo
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about 2/3 Times 2/3 Times 2/3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.