2 3 Is What Percent
straightsci
Sep 08, 2025 · 5 min read
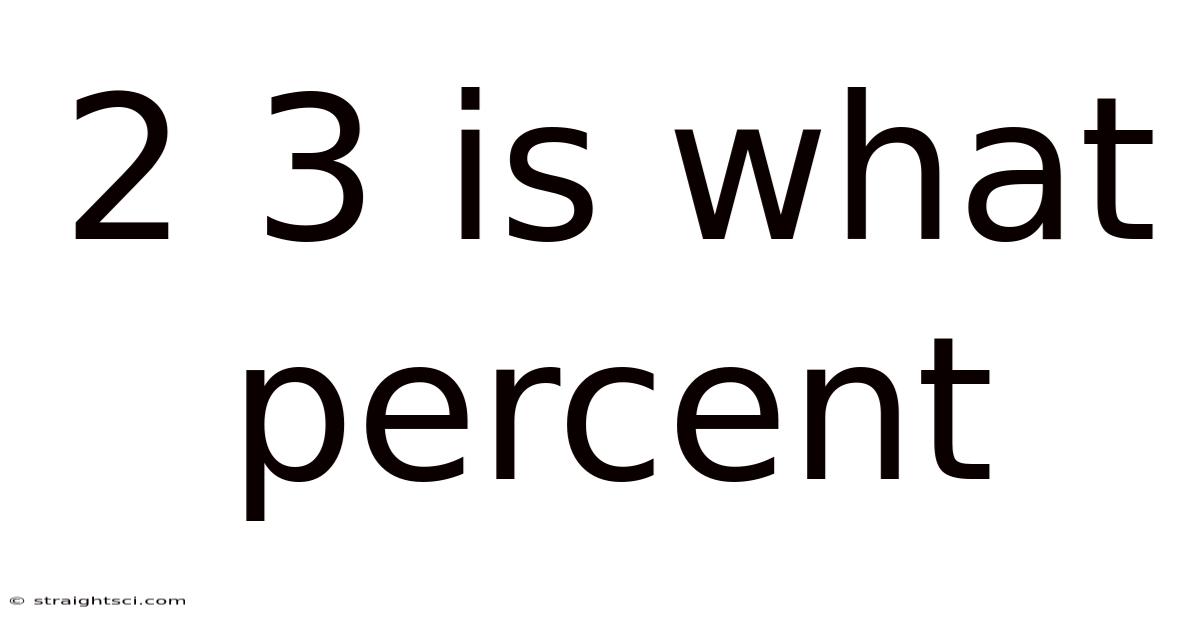
Table of Contents
Decoding Percentages: Understanding "2 is What Percent of 3?" and Beyond
Understanding percentages is a fundamental skill in mathematics with wide-ranging applications in everyday life, from calculating discounts and taxes to comprehending statistics and financial reports. This comprehensive guide will not only answer the question "2 is what percent of 3?" but also delve into the underlying principles of percentage calculations, explore various methods for solving percentage problems, and provide a solid foundation for tackling more complex percentage-related challenges. We'll also examine real-world applications and address frequently asked questions to ensure a complete understanding of this crucial mathematical concept.
What is a Percentage?
A percentage is a fraction or ratio expressed as a number out of 100. The term "percent" literally means "out of one hundred" – "per cent" being derived from the Latin "per centum." Percentages are represented using the symbol "%". For example, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or the decimal 0.5. Understanding this fundamental definition is key to solving any percentage problem.
Calculating "2 is What Percent of 3?" – The Step-by-Step Approach
Let's tackle the core question: "2 is what percent of 3?" We can solve this using several methods. Here's a step-by-step approach using the most common method:
Step 1: Set up the proportion.
We need to express the relationship between 2 and 3 as a fraction. This fraction represents the part (2) compared to the whole (3). So we have:
2/3
Step 2: Convert the fraction to a decimal.
To convert a fraction to a decimal, we divide the numerator (the top number) by the denominator (the bottom number):
2 ÷ 3 ≈ 0.6667 (We round to four decimal places for accuracy).
Step 3: Convert the decimal to a percentage.
To convert a decimal to a percentage, we multiply the decimal by 100 and add the "%" symbol:
0.6667 x 100 = 66.67%
Therefore, 2 is approximately 66.67% of 3.
Alternative Methods for Calculating Percentages
While the previous method is straightforward, there are other approaches to calculating percentages, each offering a slightly different perspective:
Method 2: Using the Formula
The percentage formula can be expressed as:
(Part / Whole) x 100% = Percentage
In our case:
(2 / 3) x 100% ≈ 66.67%
This formula directly embodies the concept of percentage as a ratio of the part to the whole.
Method 3: Cross-Multiplication
This method is particularly useful when dealing with more complex percentage problems. We can set up a proportion:
x/100 = 2/3
Cross-multiplying gives us:
3x = 200
Solving for x:
x = 200/3 ≈ 66.67%
Understanding the Concept of "Is What Percent Of"
The phrase "is what percent of" essentially asks us to find the percentage one number represents relative to another. It's crucial to identify the "part" and the "whole" correctly. The "part" is the number that represents a portion of the whole, and the "whole" is the total amount. In our example, 2 is the part, and 3 is the whole.
Real-World Applications of Percentage Calculations
Understanding percentages is vital in various aspects of life:
- Finance: Calculating interest rates, discounts, taxes, and profit margins.
- Shopping: Determining savings from sales and discounts.
- Statistics: Interpreting data and understanding probabilities.
- Science: Expressing experimental results and analyzing data.
- Everyday life: Calculating tips, splitting bills, and understanding proportions.
Advanced Percentage Problems and Techniques
While the example "2 is what percent of 3" is relatively straightforward, percentage problems can become more complex. Here are some examples:
- Finding the whole: "15% of what number is 6?" This requires rearranging the percentage formula to solve for the "whole."
- Finding the part: "What is 25% of 80?" This involves directly applying the percentage formula.
- Percentage increase/decrease: Calculating the percentage change between two values, such as price increases or population growth. This often involves finding the difference between the two values and then expressing this difference as a percentage of the original value.
- Compound interest: Calculating interest that is earned not only on the principal amount but also on the accumulated interest. This requires more advanced mathematical formulas.
Solving these more complex problems often involves algebraic manipulation of the basic percentage formula.
Frequently Asked Questions (FAQ)
Q1: Why do we multiply by 100 when converting a decimal to a percentage?
A1: We multiply by 100 because a percentage represents a fraction out of 100. Multiplying by 100 effectively scales the decimal to express the fraction as a number out of 100.
Q2: What if the "part" is larger than the "whole"?
A2: If the "part" is larger than the "whole," the resulting percentage will be greater than 100%. This indicates that the "part" represents more than the entire "whole," which is possible in certain contexts. For example, if you invested $1000 and your investment grew to $1200, the percentage increase would be more than 100%.
Q3: How do I handle percentages with decimals?
A3: Handle decimals in the same way you would handle whole numbers. Simply apply the same formula, ensuring accurate calculations.
Q4: Are there any online tools or calculators to help with percentage calculations?
A4: Yes, many online calculators and tools are available to assist with percentage calculations. These can be helpful for quick calculations or for verifying your work. However, understanding the underlying principles is crucial for problem-solving and application in various contexts.
Conclusion: Mastering Percentages
Mastering percentage calculations is a crucial skill that extends far beyond the classroom. It's a fundamental building block for understanding and navigating various aspects of everyday life, from financial matters to data interpretation. By understanding the underlying principles, the different methods for calculation, and the various applications, you can confidently tackle any percentage-related problem and apply this crucial mathematical skill to your advantage. Remember the key formula: (Part / Whole) x 100% = Percentage, and practice applying it to different scenarios to build your proficiency. The ability to confidently work with percentages will serve you well in numerous contexts, empowering you to make informed decisions and solve practical problems efficiently.
Latest Posts
Latest Posts
-
Density Of Water In Lbm Ft3
Sep 08, 2025
-
50g Of Butter To Tbsp
Sep 08, 2025
-
What Does Sro Stand For
Sep 08, 2025
-
Lewis Dot Structure For Sodium
Sep 08, 2025
-
Bid Means In Medical Terms
Sep 08, 2025
Related Post
Thank you for visiting our website which covers about 2 3 Is What Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.