2 3 4 X 2
straightsci
Aug 29, 2025 · 6 min read
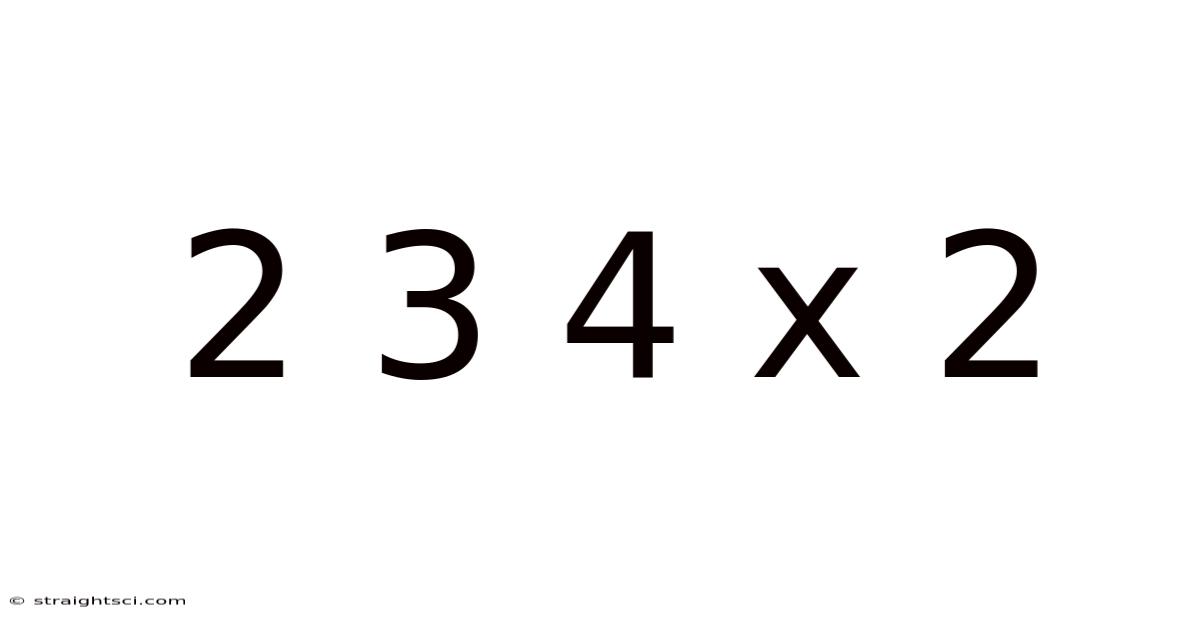
Table of Contents
Decoding 2 3 4 x 2: A Deep Dive into Mathematical Operations and Problem-Solving
This article delves into the seemingly simple mathematical expression "2 3 4 x 2," exploring its different interpretations, the order of operations (PEMDAS/BODMAS), and the broader implications for understanding mathematical problem-solving. We'll move beyond the basic calculation to discuss the importance of clarity, precision, and the various ways ambiguity can be addressed in mathematics. Understanding this seemingly simple equation opens doors to a richer appreciation of mathematical reasoning and logic.
Introduction: The Ambiguity and the Power of Parentheses
At first glance, "2 3 4 x 2" appears straightforward. However, the absence of explicit operators (+, -, ×, ÷) between the numbers introduces ambiguity. Different interpretations lead to different results. This ambiguity highlights the crucial role of notation and the importance of specifying the intended order of operations. This seemingly simple equation serves as an excellent example of why clear and unambiguous mathematical notation is paramount, especially in complex calculations and programming.
Understanding Order of Operations (PEMDAS/BODMAS)
The standard order of operations, often remembered by the acronyms PEMDAS (Parentheses, Exponents, Multiplication and Division, Addition and Subtraction) or BODMAS (Brackets, Orders, Division and Multiplication, Addition and Subtraction), dictates the sequence in which operations should be performed. The absence of parentheses or explicit operators in "2 3 4 x 2" necessitates careful consideration of this order. Without parentheses, we must adhere strictly to PEMDAS/BODMAS.
Interpretation 1: Treating the Numbers as Concatenated
One possible interpretation is to treat the numbers "2 3 4" as a single number, 234. In this case, the calculation becomes:
234 x 2 = 468
This interpretation assumes that the spacing is merely a stylistic choice and doesn't signify separate mathematical operations. While valid, it's not the most likely interpretation given the common mathematical practices of using explicit operators.
Interpretation 2: Implicit Multiplication and Addition
A second interpretation involves assuming implicit multiplication between the numbers. This could be interpreted in a few ways:
-
Option A: Left to Right: We could perform the operations from left to right, treating spaces as multiplication: (2 x 3) x 4 x 2 = 48.
This approach treats each space as a multiplication sign, simplifying to a series of consecutive multiplications.
-
Option B: Grouping with Implicit Parentheses: We could add implicit parentheses to group operations differently. For example:
2 + (3 x 4) x 2 = 2 + 12 x 2 = 26
This relies on interpreting the spacing to imply the multiplication of 3 and 4 before adding 2 and multiplying by 2. However, this approach, too, is arbitrary and dependent on interpretation, lacking explicit clarity.
-
Option C: Alternative Groupings: We could explore other groupings as well, leading to many more possible outcomes which again, highlight the necessity for clear mathematical notation.
Interpretation 3: A Case for Ambiguity and Mathematical Precision
The ambiguity inherent in "2 3 4 x 2" underscores the vital role of explicit mathematical notation. In formal mathematics, such ambiguous expressions are unacceptable. The importance of using parentheses, brackets, and clear operators (+, -, ×, ÷) cannot be overstated. This is crucial not only for obtaining the correct answer but also for ensuring clarity and avoiding misunderstandings.
The Importance of Parentheses and Brackets
Parentheses ( ) and brackets [ ] are used to group terms and explicitly dictate the order of operations. By incorporating parentheses, we can eliminate ambiguity and ensure a single, unambiguous interpretation of the expression.
For example, the following expressions have clear and distinct meanings:
- (2 + 3) x 4 x 2 = 40
- 2 + (3 x 4) x 2 = 26
- 2 + 3 x (4 x 2) = 26
- (2 + 3 + 4) x 2 = 18
- 2 + 3 + 4 x 2 = 12
These examples illustrate how different placements of parentheses radically alter the resulting value. Using parentheses is crucial to maintain clarity and ensure the correct interpretation of the expression.
Extending the Concept: Applications in Programming and Real-World Scenarios
The need for unambiguous mathematical expressions extends far beyond theoretical calculations. In programming, for instance, the order of operations is strictly defined, and the use of parentheses is crucial to avoid errors and ensure correct program execution. Similarly, in engineering, scientific applications, and even everyday accounting, clear communication through mathematical notation prevents errors that can have significant consequences.
Explanation of the Underlying Mathematical Principles:
The principles at play here aren't limited to basic arithmetic. They touch upon core concepts of mathematical logic and the formalization of mathematical operations. Understanding the order of operations, the roles of different operators, and how parentheses modify those operations are foundations that support more complex mathematical concepts learned in algebra, calculus, and beyond. Every mathematical statement requires a well-defined structure and logic to avoid ambiguity and ensure accurate outcomes.
Frequently Asked Questions (FAQ)
-
Q: What is the correct answer to 2 3 4 x 2?
A: There's no single "correct" answer without additional clarifying information. The expression is inherently ambiguous due to the lack of explicit operators and the missing parentheses.
-
Q: Why is proper notation important in mathematics?
A: Proper notation ensures clear communication and unambiguous interpretation of mathematical expressions, preventing errors and misunderstandings. It is the backbone of logical and consistent mathematical reasoning.
-
Q: How can I avoid ambiguity in my mathematical expressions?
A: Always use explicit operators (+, -, ×, ÷) and parentheses ( ) or brackets [ ] to group terms and clearly indicate the intended order of operations.
-
Q: What are some real-world examples where clear mathematical notation is vital?
A: Clear mathematical notation is essential in many fields, including programming, engineering, finance, and scientific research. Incorrect notation can lead to flawed computations, erroneous conclusions, and potentially catastrophic consequences in real-world applications.
Conclusion: The Power of Precision in Mathematics
The seemingly simple expression "2 3 4 x 2" serves as a powerful reminder of the importance of clear, unambiguous mathematical notation. The absence of explicit operators and parentheses introduces significant ambiguity, leading to multiple possible interpretations and results. This underscores the crucial role of the order of operations (PEMDAS/BODMAS) and the necessity of using parentheses and brackets to group terms and dictate the sequence of calculations. Mastering these fundamental principles is essential for success in mathematics and related fields, fostering a more profound appreciation of precision and clarity in problem-solving. Understanding this principle moves you beyond simple calculations and into a deeper understanding of mathematical logic and the fundamental structure of mathematics. The emphasis on clear notation transcends simple arithmetic and extends to all aspects of mathematics, providing a solid foundation for tackling more complex concepts in the future. The lesson of precision learned from this simple expression is a cornerstone of mathematical understanding and problem-solving at any level.
Latest Posts
Latest Posts
-
How Many Atoms In Molecule
Aug 29, 2025
-
Equation For Discharging A Capacitor
Aug 29, 2025
-
Solving Linear Systems By Substitution
Aug 29, 2025
-
Periodic Table With Color Coding
Aug 29, 2025
-
What Is Counts Per Minute
Aug 29, 2025
Related Post
Thank you for visiting our website which covers about 2 3 4 X 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.