2 2/3 Divided By 3
straightsci
Sep 13, 2025 · 6 min read
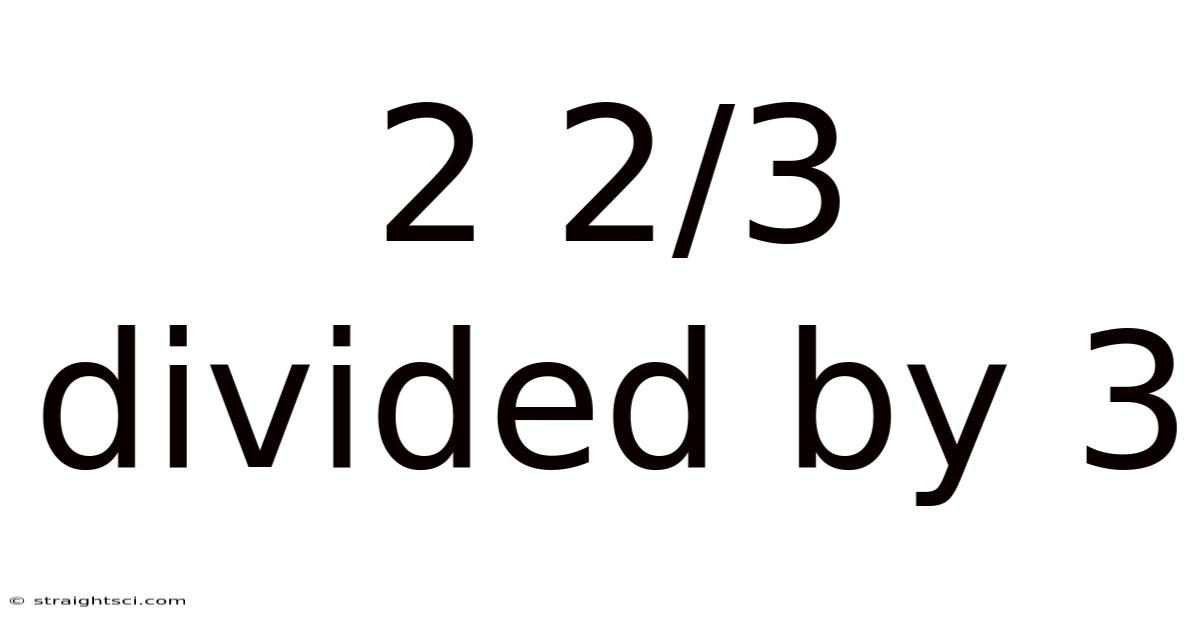
Table of Contents
Diving Deep into Division: Solving 2 2/3 ÷ 3
Understanding division, especially when dealing with mixed numbers like 2 2/3, can seem daunting at first. This comprehensive guide will walk you through the process of solving 2 2/3 divided by 3, explaining the underlying principles and providing multiple approaches to reach the solution. Whether you're a student struggling with fractions or simply looking to refresh your math skills, this article will equip you with the knowledge and confidence to tackle similar problems. We'll explore the mechanics of the calculation, delve into the underlying mathematical concepts, and answer frequently asked questions.
Understanding the Problem: 2 2/3 ÷ 3
The problem, 2 2/3 ÷ 3, asks us to determine how many times the number 3 fits into the quantity 2 2/3. This seemingly simple problem requires a grasp of several key mathematical concepts: fractions, mixed numbers, and division itself. We'll break down each of these components before tackling the calculation.
A Primer on Fractions and Mixed Numbers
Before we begin dividing, let's solidify our understanding of the fundamental building blocks of our problem: fractions and mixed numbers.
-
Fractions: A fraction represents a part of a whole. It consists of two numbers: the numerator (top number) and the denominator (bottom number). The numerator indicates the number of parts we have, while the denominator indicates the total number of parts the whole is divided into. For example, in the fraction 2/3, the numerator is 2 and the denominator is 3. This means we have 2 out of 3 equal parts.
-
Mixed Numbers: A mixed number combines a whole number and a fraction. For instance, 2 2/3 means we have two whole units and an additional 2/3 of a unit.
Converting Mixed Numbers to Improper Fractions: The Key to Easier Division
Dividing mixed numbers directly can be cumbersome. The most efficient strategy is to convert the mixed number into an improper fraction. An improper fraction is a fraction where the numerator is greater than or equal to the denominator. This representation simplifies the division process significantly.
To convert 2 2/3 into an improper fraction, we follow these steps:
- Multiply the whole number by the denominator: 2 * 3 = 6
- Add the numerator to the result: 6 + 2 = 8
- Keep the same denominator: 3
Therefore, 2 2/3 is equivalent to the improper fraction 8/3.
Method 1: Dividing Improper Fractions
Now that we've transformed our mixed number into an improper fraction, we can proceed with the division:
8/3 ÷ 3
Dividing by a whole number is the same as multiplying by its reciprocal. The reciprocal of 3 is 1/3. So our problem becomes:
8/3 * 1/3
To multiply fractions, we multiply the numerators together and the denominators together:
(8 * 1) / (3 * 3) = 8/9
Therefore, 2 2/3 divided by 3 equals 8/9.
Method 2: Breaking Down the Division – A Visual Approach
Another way to approach this problem is to visualize the division process. We are dividing 2 2/3 into three equal parts. Let’s break it down:
-
Divide the whole numbers: If we divide the two whole units into three parts, we can't do this evenly. This means each part will get less than one whole unit.
-
Divide the fraction: Now, let’s focus on the fractional part, 2/3. Dividing 2/3 into three equal parts means each part will get (2/3) / 3 = 2/9.
-
Combining the results: Each of the three parts will contain less than a whole unit, specifically 2/9. Since we started with two whole units, we need to consider how much of each whole unit contributes to each of the three parts. Each whole unit contributes 1/3 to each part. With two whole units, we have a total contribution of 2/3 to each part. Adding this to the fractional contribution (2/9), we get: 2/3 + 2/9 = 6/9 + 2/9 = 8/9.
This visual approach confirms our previous result: 8/9.
Method 3: Using Decimal Equivalents
While working with fractions is crucial for a solid mathematical foundation, we can also solve this problem using decimal equivalents.
First, convert the mixed number 2 2/3 into a decimal:
2 + (2 ÷ 3) ≈ 2 + 0.6667 = 2.6667
Now, divide this decimal by 3:
2.6667 ÷ 3 ≈ 0.8889
This decimal, 0.8889, is approximately equal to 8/9. Note that using decimals introduces a small degree of approximation due to the repeating decimal nature of 2/3.
The Importance of Understanding Different Methods
Presenting multiple methods is not just about redundancy; it's about building a deeper understanding. Each approach emphasizes different aspects of the problem, enhancing your overall comprehension of fractional division. The fractional method provides a precise answer and reinforces fundamental fraction manipulation skills. The visual method promotes a more intuitive grasp of the division process, while the decimal method highlights the connection between fractions and decimals. Mastering all these approaches will make you a more versatile and confident problem-solver.
Frequently Asked Questions (FAQs)
Q1: Can I divide the whole number and fraction separately?
A1: While tempting, dividing the whole number and the fraction separately will not give you the correct answer in most cases. You must first convert the mixed number to an improper fraction before performing the division, ensuring that you're working with the entire quantity.
Q2: What if I have a more complex mixed number?
A2: The process remains the same. Convert the mixed number to an improper fraction and then perform the division using the methods described above. The more you practice, the more comfortable you'll become with these manipulations.
Q3: Why is converting to an improper fraction essential?
A3: Converting to an improper fraction streamlines the division process. It eliminates the need for separate calculations with the whole number and fractional parts, leading to a more efficient and accurate solution.
Q4: Are there any other ways to represent the answer?
A4: Yes, besides 8/9, you could also express the answer as a decimal (approximately 0.8889) or as a percentage (approximately 88.89%). The best representation depends on the context of the problem.
Conclusion: Mastering Fractional Division
Solving 2 2/3 ÷ 3, seemingly a simple problem, unveils the essential concepts of fractions, mixed numbers, and division. By understanding the conversion of mixed numbers to improper fractions and employing different calculation methods, you've gained valuable insight into manipulating fractions effectively. Remember, consistent practice and understanding the underlying principles are key to mastering these mathematical concepts. With continued practice, tackling more complex fractional division problems will become increasingly easier and more intuitive. You've now taken a significant step towards developing a strong foundation in mathematics!
Latest Posts
Latest Posts
-
Is Austria Similar To Germany
Sep 14, 2025
-
Is Nacl Ionic Or Covalent
Sep 14, 2025
-
Buffer Zone On Titration Curve
Sep 14, 2025
-
Vertex Formula For Quadratic Equation
Sep 14, 2025
-
What Is A Polyatomic Compound
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about 2 2/3 Divided By 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.