1 X 2 Y 2
straightsci
Sep 22, 2025 · 6 min read
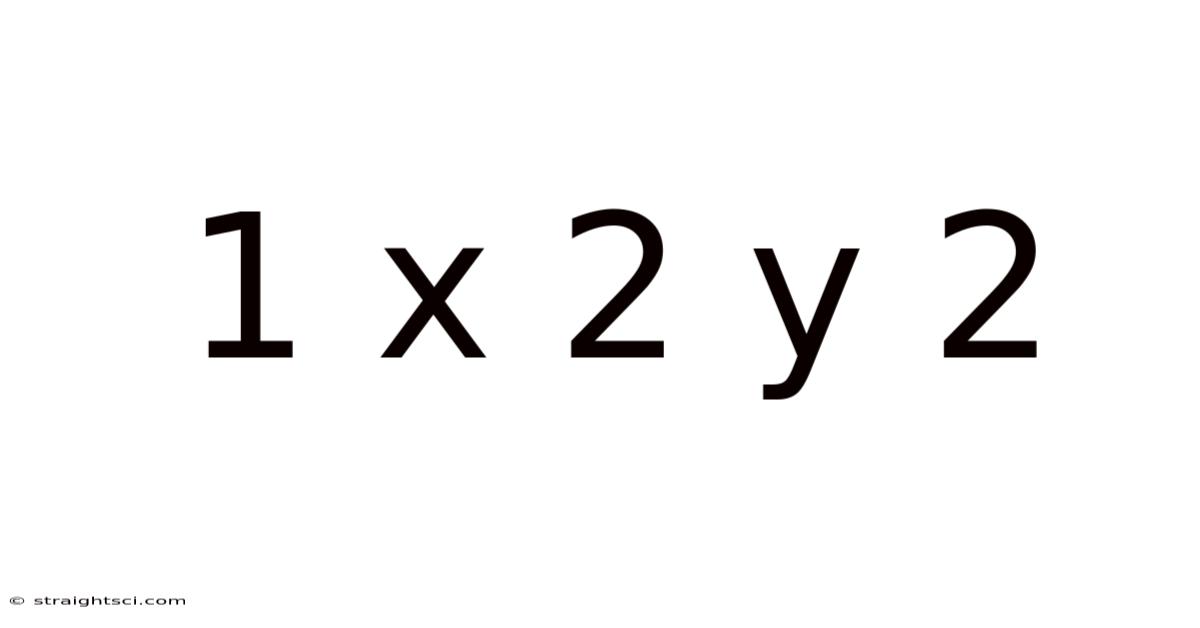
Table of Contents
Decoding 1x2y²: A Deep Dive into Quadratic Equations and Their Applications
The expression "1x² + 2y²" might seem simple at first glance, but it actually opens the door to a fascinating world of mathematics, specifically quadratic equations and their numerous applications in various fields. This seemingly basic algebraic expression represents a crucial component within a broader mathematical landscape, offering insights into conic sections, optimization problems, and even physics. Understanding its nuances provides a solid foundation for tackling more complex mathematical concepts. This article will explore this expression in detail, breaking down its components, demonstrating its applications, and addressing frequently asked questions.
Introduction to Quadratic Equations and Variables
Before delving into the specifics of "1x² + 2y²," let's establish a fundamental understanding of quadratic equations. A quadratic equation is a polynomial equation of the second degree, meaning the highest power of the variable is 2. The general form of a quadratic equation in one variable is ax² + bx + c = 0, where 'a', 'b', and 'c' are constants, and 'a' is not equal to zero. Our expression, "1x² + 2y²," doesn't fit this exact form because it involves two variables, x and y. This makes it a quadratic expression rather than a quadratic equation (equations require an equals sign and a value). However, the underlying principles of quadratic equations are still highly relevant.
The 'x' and 'y' represent variables, meaning they can take on various numerical values. The coefficients, '1' and '2', indicate the multiplicative factors associated with each term. The squared terms (x² and y²) are essential characteristics of quadratic expressions and equations, defining their parabolic nature.
Understanding the Geometric Representation: Conic Sections
The expression "1x² + 2y²" is closely related to the geometry of conic sections. If we set this expression equal to a constant, say 'k' (1x² + 2y² = k), we obtain an equation that describes an ellipse.
-
Ellipses: Ellipses are characterized by two focal points. The sum of the distances from any point on the ellipse to these two focal points remains constant. The equation 1x² + 2y² = k represents an ellipse where the lengths of the semi-major and semi-minor axes are determined by the value of 'k'. A larger 'k' value results in a larger ellipse, while a smaller 'k' results in a smaller ellipse. The specific shape of the ellipse depends on the ratio of the coefficients (1 and 2 in this case).
-
Circles (Special Case): If the coefficients of x² and y² were equal (e.g., x² + y² = k), the equation would represent a circle, a special case of an ellipse where both focal points coincide at the center.
-
Other Conic Sections: While "1x² + 2y²" primarily relates to ellipses, variations of this expression can represent other conic sections like parabolas and hyperbolas. For example, if we had an equation of the form x² = 4py (a parabola) or x²/a² - y²/b² = 1 (a hyperbola), the underlying principles of quadratic equations are still in play, but the geometric shapes are different.
Applications of Quadratic Expressions and Equations
The principles illustrated by the expression "1x² + 2y²," and the broader realm of quadratic equations, find extensive applications in numerous fields:
-
Physics: Quadratic equations are fundamental to describing projectile motion. The trajectory of a projectile under the influence of gravity follows a parabolic path, perfectly described by quadratic equations relating distance, time, velocity, and acceleration.
-
Engineering: In structural engineering, quadratic equations are used to model the stress and strain on structures. Understanding the behavior of materials under stress often requires solving quadratic equations. Similarly, in electrical engineering, quadratic equations appear in circuit analysis.
-
Economics and Finance: Quadratic functions can model various economic phenomena, such as cost functions, revenue functions, and profit functions. Finding optimal values (e.g., maximizing profit) often involves solving quadratic equations.
-
Computer Graphics and Game Development: Quadratic curves are widely used to create realistic and smooth curves in computer graphics and game development. The parabolic arcs in animations, for example, rely on quadratic equations.
-
Optimization Problems: Many real-world problems involve finding the maximum or minimum value of a function. If the function is quadratic, solving the corresponding equation provides the solution. This has applications in areas like operations research, logistics, and resource allocation.
Solving Quadratic Equations: Techniques and Methods
While "1x² + 2y²" isn't an equation in the standard form to be solved in the same way as ax² + bx + c = 0, understanding how to solve quadratic equations is crucial for related problems. Here are some common methods:
-
Factoring: This involves expressing the quadratic expression as a product of two linear expressions. This method is most efficient when the quadratic equation can be easily factored.
-
Quadratic Formula: This formula provides a direct solution for any quadratic equation: x = [-b ± √(b² - 4ac)] / 2a. This formula is universally applicable, regardless of the factors' ease of calculation.
-
Completing the Square: This method involves manipulating the quadratic expression to create a perfect square trinomial, making it easier to solve.
-
Graphing: Graphing the quadratic equation allows for visualization of the solutions (x-intercepts, where the graph intersects the x-axis).
Extending the Concept: Multivariable Quadratic Forms
The expression "1x² + 2y²" can be seen as a simple example of a quadratic form. A quadratic form involves a sum of squared terms, possibly with cross-terms (terms involving xy). In matrix notation, quadratic forms can be represented concisely, enabling more sophisticated analysis. This is essential in areas like linear algebra and multivariate calculus.
Frequently Asked Questions (FAQ)
-
Q: What is the difference between a quadratic equation and a quadratic expression?
-
A: A quadratic equation is a complete statement with an equals sign, showing a relationship between the expression and a specific value (e.g., x² + 2x + 1 = 0). A quadratic expression is simply an algebraic expression containing a variable raised to the second power (e.g., x² + 2x + 1).
-
Q: Can I solve "1x² + 2y² = k" for x and y?
-
A: You can't solve for unique values of x and y without additional information or constraints. This equation represents an ellipse; for each value of x, there are two corresponding values of y (and vice-versa), unless the equation is further constrained or another condition is imposed.
-
Q: What is the significance of the coefficients (1 and 2) in the expression?
-
A: The coefficients determine the shape and scale of the conic section represented by the equation when set to a constant. In our case, it defines the specific ellipse formed. Different coefficients would lead to different ellipses.
-
Q: How does this relate to calculus?
-
A: Quadratic functions are fundamental in calculus. Finding the maximum or minimum values of a quadratic function using differentiation is a common application of calculus. The derivative of a quadratic function is a linear function, simplifying the process of finding critical points.
Conclusion: The Richness of Quadratic Expressions
The seemingly simple expression "1x² + 2y²" serves as a gateway to understanding the broader world of quadratic equations and their profound implications. From the geometric beauty of conic sections to their practical applications in various scientific and engineering disciplines, quadratic equations are integral to many aspects of our world. By grasping the fundamentals outlined here, you equip yourself with a crucial tool for tackling more complex mathematical challenges and appreciating the elegance of mathematical relationships. Further exploration of quadratic forms, matrix representation, and their applications in multivariate calculus will solidify your understanding of this essential concept.
Latest Posts
Latest Posts
-
What Is A Radioactive Isotope
Sep 22, 2025
-
Whats 55 Kg In Pounds
Sep 22, 2025
-
Where Was The Mayan Empire
Sep 22, 2025
-
Answers On Magic 8 Ball
Sep 22, 2025
-
2 X 1 2 3
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 1 X 2 Y 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.