1 X 1 1 3
straightsci
Sep 23, 2025 · 6 min read
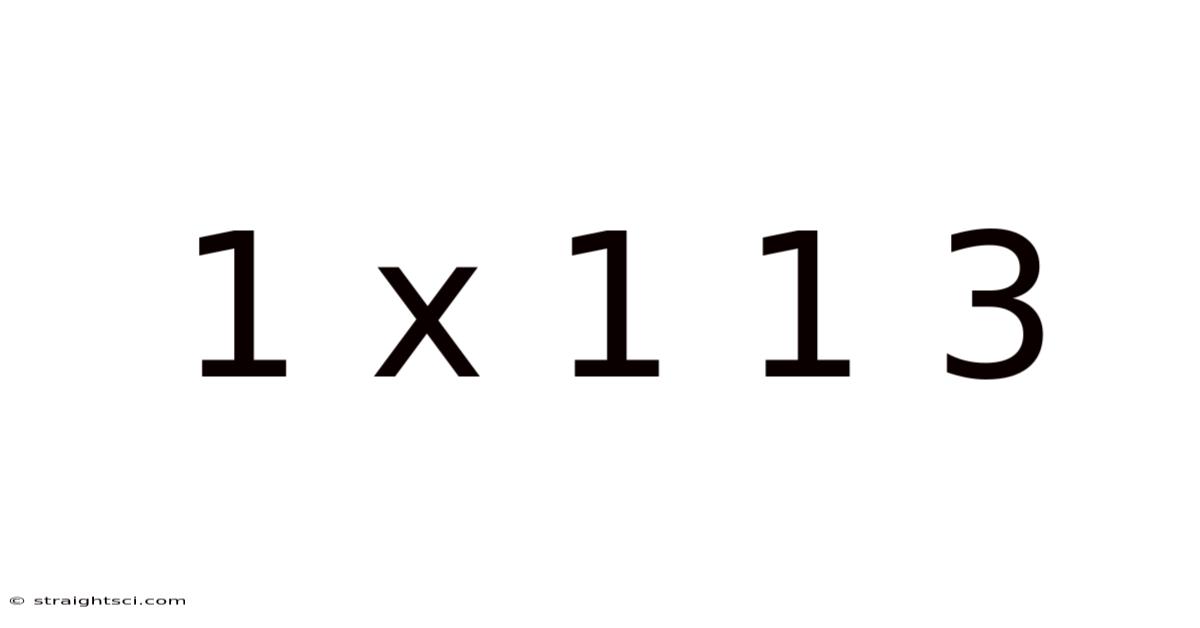
Table of Contents
Unraveling the Mystery of 1 x 1 = 1, 1 + 1 = 2, and the Implications of Simple Arithmetic
This article delves into the seemingly simple yet profoundly significant world of basic arithmetic, specifically focusing on the equations 1 x 1 = 1 and 1 + 1 = 2. While these might appear trivial at first glance, they form the bedrock of mathematics and hold implications far beyond simple calculations. We'll explore their foundational role, delve into their applications in various fields, and even touch upon some of the philosophical questions they raise. Understanding these fundamental concepts is crucial for anyone seeking a deeper appreciation of mathematics and its pervasive influence on our lives.
Introduction: The Building Blocks of Arithmetic
At the heart of mathematics lie the fundamental operations: addition, subtraction, multiplication, and division. These four operations are the building blocks upon which all other mathematical concepts are constructed. The equations 1 x 1 = 1 and 1 + 1 = 2 represent the most elementary applications of multiplication and addition respectively, using the smallest positive integer, 1. Their simplicity, however, belies their profound importance. These equations aren't just about getting the right answer; they are about understanding the underlying principles of number systems and operations.
1 x 1 = 1: Multiplication as Repeated Addition
The equation 1 x 1 = 1 embodies the essence of multiplication. Multiplication can be understood as repeated addition. For example, 3 x 2 means adding 2 three times: 2 + 2 + 2 = 6. In the case of 1 x 1, it means adding 1 one time, resulting in 1. This simple example highlights the identity property of multiplication: any number multiplied by 1 equals itself. This seemingly basic property is crucial in many mathematical contexts, providing a foundation for more complex operations and calculations.
-
Identity Property of Multiplication: This property states that for any number a, a x 1 = a and 1 x a = a. This property simplifies calculations and is fundamental in algebra and beyond.
-
Understanding the Concept of "One": The number 1 represents a single unit, a fundamental building block in counting and measurement. Its unique properties in multiplication and other operations are essential for constructing more complex mathematical systems.
1 + 1 = 2: Addition and the Concept of Sets
The equation 1 + 1 = 2 showcases the fundamental operation of addition. Addition represents the combining of quantities. In set theory, adding 1 + 1 can be visualized as combining two sets, each containing one element. The result is a new set containing two elements. This seemingly simple act of combining lays the groundwork for understanding larger sums and more complex mathematical structures.
-
Set Theory: The concept of sets is fundamental in mathematics and computer science. A set is a collection of distinct objects. Adding sets together represents the union of those sets.
-
Cardinality: The number of elements in a set is called its cardinality. 1 + 1 = 2 demonstrates that the cardinality of the union of two sets, each with cardinality 1, is 2.
Beyond the Basics: Applications in Advanced Mathematics
While seemingly rudimentary, the principles embedded in 1 x 1 = 1 and 1 + 1 = 2 extend far beyond elementary arithmetic. These simple equations form the basis for:
-
Algebra: These fundamental operations are the building blocks of algebraic manipulations. Solving equations, simplifying expressions, and working with variables all rely on the understanding of these basic operations.
-
Calculus: Calculus, the study of change, relies heavily on the concepts of limits and infinitesimals. While these concepts are complex, they build upon the foundational understanding of addition and multiplication. The accumulation of infinitesimally small changes fundamentally relies on the concept of repeated addition.
-
Linear Algebra: Linear algebra, which involves the study of vectors and matrices, uses addition and multiplication as core operations. Vector addition and scalar multiplication are directly derived from these fundamental concepts.
-
Number Theory: Number theory explores the properties of numbers themselves. The simplicity of 1 plays a critical role in theorems and proofs related to prime numbers, modular arithmetic, and other advanced topics.
Philosophical Implications: The Nature of Numbers and Counting
The simplicity of 1 + 1 = 2 has also sparked philosophical discussion. The statement seems self-evident, yet its underlying assumptions raise questions about the nature of numbers and the act of counting itself. Consider these points:
-
The Peano Axioms: These axioms, fundamental to set theory, define the natural numbers and their properties. The axiom that states "1 is a natural number" and the successor axiom (every natural number has a unique successor) form the foundation for all other natural numbers, including the derivation of 2 as the successor of 1.
-
The Foundations of Mathematics: The seemingly simple equations of 1 x 1 = 1 and 1 + 1 = 2 underscore the need for rigorous foundational systems in mathematics. These systems ensure consistency and prevent paradoxes. The development of formal axiomatic systems, like Peano arithmetic and Zermelo-Fraenkel set theory, addresses this need.
-
The Objectivity of Mathematics: The seemingly objective truth of 1 + 1 = 2 leads to discussions on the objectivity of mathematical truths. Are mathematical truths discovered or created? This question remains a topic of ongoing debate among mathematicians and philosophers.
Frequently Asked Questions (FAQ)
Q: Are these equations always true?
A: Within the standard number systems (natural numbers, integers, real numbers, etc.), these equations are universally true. However, in some unconventional or abstract mathematical systems, the properties of 1 and the definitions of addition and multiplication may differ, leading to different results.
Q: What is the significance of the number 1?
A: The number 1 holds unique significance. It's the multiplicative identity (any number multiplied by 1 remains unchanged), it is the smallest positive integer, and it serves as the foundation for counting and constructing other numbers.
Q: Are there any exceptions to 1 + 1 = 2?
A: Within standard mathematical systems, there are no exceptions. However, in fields like quantum mechanics, where concepts like superposition exist, the simple summation of quantities might not always directly translate to the classical understanding of addition. This doesn't invalidate 1 + 1 = 2 within its standard mathematical context.
Conclusion: A Foundation for All of Mathematics
The equations 1 x 1 = 1 and 1 + 1 = 2 may appear elementary, but they are far from trivial. They represent the fundamental building blocks of mathematics, forming the basis for more advanced concepts and applications across various disciplines. Their simplicity belies their profound importance in establishing the consistent and logical framework of mathematics. Understanding these basic principles is crucial not only for mathematical proficiency but also for appreciating the power and elegance of mathematical reasoning and its influence on our understanding of the world around us. The seemingly simple act of adding or multiplying the smallest positive integer lays the groundwork for the complex and beautiful structure of mathematics as a whole. From the simplest calculations to the most sophisticated theories, the principles embodied in these fundamental equations remain unwavering.
Latest Posts
Latest Posts
-
74 Degrees Fahrenheit To Celsius
Sep 23, 2025
-
Endothermic Reaction Vs Exothermic Reaction
Sep 23, 2025
-
What Is The Worlds Population
Sep 23, 2025
-
What Perimeter Of A Rectangle
Sep 23, 2025
-
What Is Seal In French
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about 1 X 1 1 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.