1/square Root Of X Derivative
straightsci
Sep 17, 2025 · 6 min read
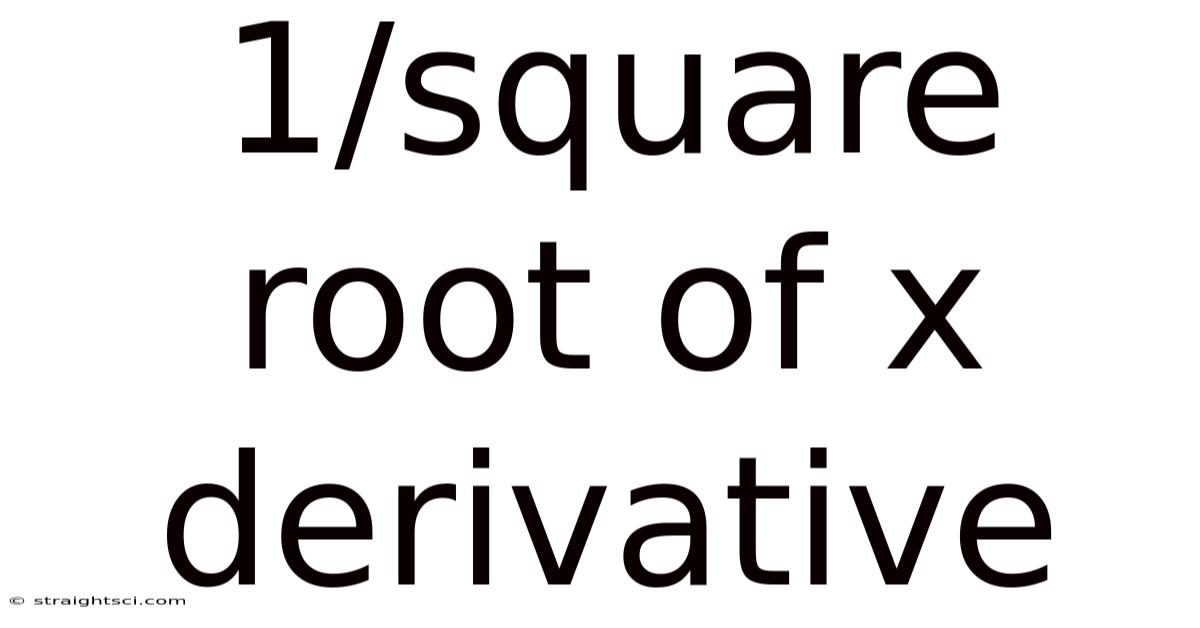
Table of Contents
Understanding the Derivative of 1/√x: A Comprehensive Guide
Finding the derivative of functions is a cornerstone of calculus. This article delves into the process of finding the derivative of 1/√x, exploring various methods, providing a step-by-step explanation, and clarifying common misconceptions. We'll also touch upon the broader applications of this derivative in various fields. This guide aims to equip you with a thorough understanding, whether you're a student grappling with calculus or a professional seeking a refresher.
Understanding the Function: 1/√x
Before diving into the derivative, let's clarify the function itself: 1/√x. This can also be written as x<sup>-1/2</sup>. This representation is crucial because it simplifies the application of power rule, a fundamental tool in differential calculus. The function represents a reciprocal square root function, defined for all positive values of x (x > 0) since the square root of a negative number is not a real number. Its graph shows a curve that approaches infinity as x approaches 0 and gradually decreases as x increases. Understanding the nature of this function is essential for comprehending its derivative.
Method 1: Applying the Power Rule
The power rule is a simple yet powerful tool for finding the derivative of functions in the form x<sup>n</sup>, where 'n' is any real number. The rule states that the derivative of x<sup>n</sup> is nx<sup>n-1</sup>. Applying this to our function, x<sup>-1/2</sup>:
-
Identify the exponent: In our function, x<sup>-1/2</sup>, the exponent 'n' is -1/2.
-
Apply the power rule: Multiply the function by the exponent and then subtract 1 from the exponent.
d/dx (x<sup>-1/2</sup>) = (-1/2)x<sup>(-1/2 - 1)</sup> = (-1/2)x<sup>-3/2</sup>
-
Simplify the result: We can rewrite this as -1/(2x<sup>3/2</sup>) or -1/(2√x³).
Therefore, the derivative of 1/√x is -1/(2x<sup>3/2</sup>) or -1/(2√x³).
Method 2: Using the Quotient Rule
Another approach involves using the quotient rule. The quotient rule is used to find the derivative of a function that is the quotient of two other functions. The rule states: If we have a function f(x) = g(x)/h(x), then the derivative f'(x) = [h(x)g'(x) - g(x)h'(x)] / [h(x)]².
Let's apply this to 1/√x where g(x) = 1 and h(x) = √x = x<sup>1/2</sup>:
-
Find the derivatives of g(x) and h(x):
- g'(x) = d/dx (1) = 0
- h'(x) = d/dx (x<sup>1/2</sup>) = (1/2)x<sup>-1/2</sup>
-
Apply the quotient rule:
f'(x) = [(x<sup>1/2</sup>)(0) - (1)((1/2)x<sup>-1/2</sup>)] / (x<sup>1/2</sup>)² = - (1/2)x<sup>-1/2</sup> / x = -(1/2)x<sup>-3/2</sup>
-
Simplify the result: This simplifies to -1/(2x<sup>3/2</sup>) or -1/(2√x³), the same result as using the power rule.
Method 3: Chain Rule and Implicit Differentiation (Advanced)
While the power rule and quotient rule are the most straightforward approaches, we can also use the chain rule in conjunction with implicit differentiation. This method is more complex but provides a valuable alternative understanding.
Let y = 1/√x. We can rewrite this as y√x = 1. Then, we differentiate implicitly with respect to x:
-
Differentiate both sides: d/dx (y√x) = d/dx (1) This uses the product rule on the left side: (dy/dx)√x + y(1/(2√x)) = 0
-
Solve for dy/dx: (dy/dx)√x = -y/(2√x) dy/dx = -y/(2x)
-
Substitute for y: Since y = 1/√x, we substitute this back into the equation: dy/dx = -(1/√x) / (2x) = -1/(2x√x) = -1/(2x<sup>3/2</sup>)
Again, we arrive at the same derivative: -1/(2x<sup>3/2</sup>).
Graphical Interpretation of the Derivative
The derivative of a function at a point represents the instantaneous rate of change of the function at that point. Graphically, it's the slope of the tangent line to the curve at that point. For the function 1/√x, the derivative, -1/(2x<sup>3/2</sup>), tells us that the slope of the tangent line is always negative for positive x values, indicating that the function is always decreasing. Furthermore, the magnitude of the slope decreases as x increases, meaning the curve becomes less steep as x moves further from zero.
Applications of the Derivative
The derivative of 1/√x, or more generally, derivatives of functions involving fractional exponents, have wide-ranging applications across various disciplines:
-
Physics: In describing the motion of objects, especially those involving inverse square relationships (like gravitational or electrostatic forces), derivatives of functions similar to 1/√x are frequently encountered. For instance, the rate of change of gravitational force with respect to distance involves this type of derivative.
-
Engineering: Many engineering problems, particularly in fluid dynamics and heat transfer, involve solving differential equations containing functions with fractional exponents. The derivative provides crucial information for analyzing and solving these equations.
-
Economics and Finance: In modeling various economic phenomena, functions with fractional exponents often appear. Derivatives of these functions can be used to calculate marginal costs, marginal revenue, or other key economic indicators. They are also crucial in understanding the sensitivity of certain variables in financial models.
-
Probability and Statistics: Certain probability distributions involve functions with fractional powers, and their derivatives are essential for calculating probabilities, moments, and other statistical measures.
Frequently Asked Questions (FAQ)
Q1: What is the domain of the derivative -1/(2x<sup>3/2</sup>)?
A1: Similar to the original function, the derivative is defined only for positive values of x (x > 0). The denominator cannot be zero, and a negative value would result in a complex number.
Q2: Can the derivative ever be zero?
A2: No, the derivative -1/(2x<sup>3/2</sup>) is always negative for x > 0. It approaches zero as x approaches infinity, but it never actually reaches zero.
Q3: How do I find the second derivative?
A3: To find the second derivative, we differentiate the first derivative: d²/dx² (x<sup>-1/2</sup>) = d/dx [(-1/2)x<sup>-3/2</sup>] = (3/4)x<sup>-5/2</sup> = 3/(4x<sup>5/2</sup>)
Q4: What are the practical implications of understanding this derivative?
A4: Understanding this derivative allows for the analysis of rates of change involving inverse square root relationships. This is crucial in diverse fields for modeling, optimization, and problem-solving across physics, engineering, finance, and other disciplines.
Conclusion
Finding the derivative of 1/√x, whether using the power rule, quotient rule, or the more advanced chain rule with implicit differentiation, provides a valuable exercise in understanding fundamental calculus concepts. The derivative itself, -1/(2x<sup>3/2</sup>), holds significant meaning, providing insight into the rate of change of this specific function and its broader implications across various scientific and mathematical applications. Mastering this derivative not only strengthens your calculus skills but also equips you with a powerful tool for tackling complex problems in numerous fields. Remember to practice different approaches to reinforce your understanding and build a strong foundation in calculus.
Latest Posts
Latest Posts
-
Number Of Electrons For Aluminum
Sep 17, 2025
-
Bohr Rutherford Diagram Of Boron
Sep 17, 2025
-
Periodic Table Liquid Gas Solid
Sep 17, 2025
-
How Many Inches Is 60mm
Sep 17, 2025
-
Figurative Language Vs Literal Language
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 1/square Root Of X Derivative . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.