1 E Ln 1 E
straightsci
Sep 04, 2025 · 5 min read
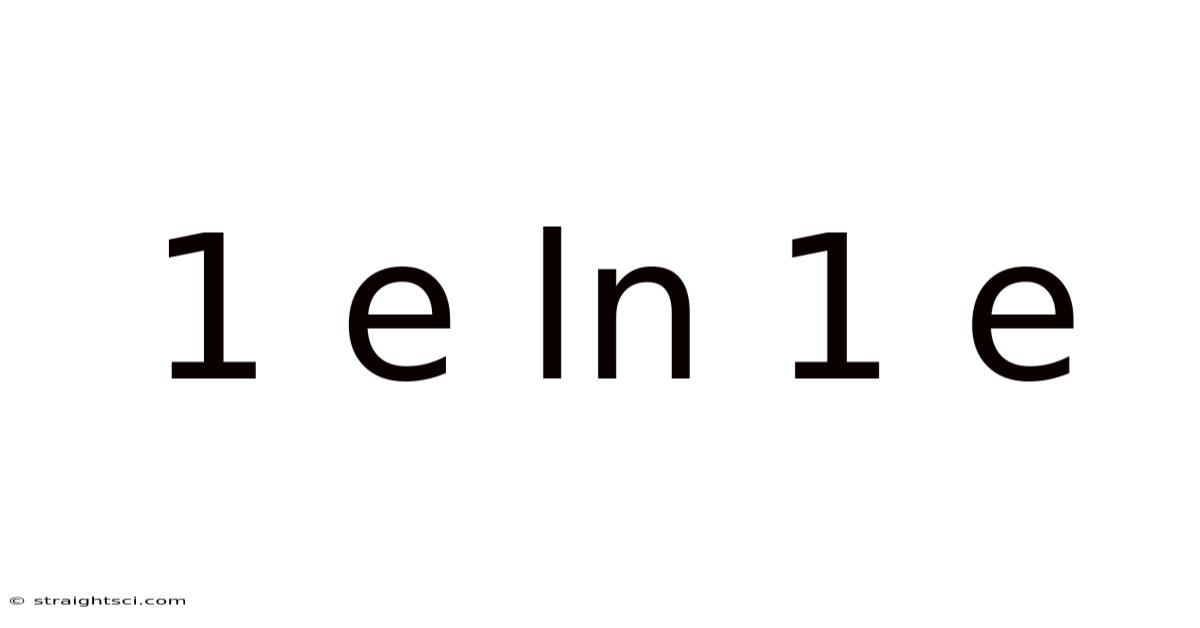
Table of Contents
Unraveling the Mystery: 1 * e^(ln 1/e)
The expression 1 * e^(ln 1/e) might seem daunting at first glance, especially for those less familiar with logarithmic and exponential functions. However, understanding this expression involves a fundamental grasp of the relationship between exponential functions and their inverse, logarithmic functions, specifically the natural logarithm (ln). This article will delve into the intricacies of this expression, providing a step-by-step solution, exploring the underlying mathematical principles, and addressing frequently asked questions. Our goal is not just to solve the equation but to foster a deeper understanding of the mathematical concepts involved.
Introduction: Understanding Exponential and Logarithmic Functions
Before tackling the expression 1 * e^(ln 1/e), let's solidify our understanding of exponential and logarithmic functions. An exponential function describes growth or decay, often represented as a^x, where 'a' is the base and 'x' is the exponent. The natural exponential function, denoted as e^x or exp(x), uses the mathematical constant e (approximately 2.71828) as its base. This constant appears naturally in many areas of mathematics and science, including compound interest and radioactive decay.
The logarithmic function is the inverse of the exponential function. It answers the question: "To what power must we raise the base to obtain a given number?" The natural logarithm, denoted as ln(x), is the logarithm with base e. Therefore, ln(x) = y is equivalent to e^y = x. This inverse relationship is crucial for solving our expression.
Step-by-Step Solution: Deconstructing 1 * e^(ln 1/e)
Let's break down the expression 1 * e^(ln 1/e) step-by-step:
-
Simplify the Argument of the Logarithm: The first step involves simplifying the argument within the natural logarithm:
1/e. This is simply the reciprocal of e. -
Apply the Logarithm Property: Recall the logarithm property:
ln(a/b) = ln(a) - ln(b). Applying this toln(1/e), we get:ln(1/e) = ln(1) - ln(e) -
Evaluate the Logarithms: We know that
ln(1) = 0(because e^0 = 1) andln(e) = 1(because e^1 = e). Substituting these values, we get:ln(1/e) = 0 - 1 = -1 -
Substitute Back into the Original Expression: Now, substitute this result back into the original expression:
1 * e^(ln 1/e) = 1 * e^(-1) -
Simplify the Exponential Expression: Recall that
e^(-1)is the same as1/e. Therefore:1 * e^(-1) = 1 * (1/e) = 1/e
Therefore, the final answer to the expression 1 * e^(ln 1/e) is 1/e.
Mathematical Explanation: The Inverse Relationship
The solution highlights the crucial inverse relationship between the exponential function (e^x) and the natural logarithm (ln(x)). The expression e^(ln x) simplifies to x because the exponential function "undoes" the logarithm. This is analogous to how addition and subtraction are inverse operations, or multiplication and division.
In our example, e^(ln(1/e)) simplifies to 1/e because the exponential function with base e cancels out the natural logarithm, leaving us with the argument of the logarithm. This principle forms the foundation for solving many complex mathematical problems involving exponential and logarithmic functions.
Further Exploration: Extending the Concepts
The principles demonstrated above can be applied to more complex expressions involving exponential and logarithmic functions. Consider these examples:
-
e^(ln(x^2)): Using the logarithm propertyln(a^b) = b * ln(a), this simplifies toe^(2ln(x)). Further simplifying using exponential properties gives use^(ln(x^2)) = (e^(ln(x)))^2 = x^2. -
ln(e^(x^3)): Similarly, the natural logarithm cancels out the exponential function, resulting inln(e^(x^3)) = x^3.
These examples illustrate the power and elegance of the inverse relationship between exponential and logarithmic functions. Mastering this relationship is key to successfully tackling numerous problems in calculus, physics, engineering, and finance.
Frequently Asked Questions (FAQ)
Q1: Why is e such an important mathematical constant?
A1: e, also known as Euler's number, is a fundamental constant that appears in various areas of mathematics and science. It arises naturally in the study of exponential growth and decay, compound interest, probability theory, and many other fields. Its unique properties, particularly its relationship with the natural logarithm, make it invaluable in mathematical modeling.
Q2: Can I use this method for logarithms with different bases?
A2: The method described above primarily applies to natural logarithms (base e). While similar principles apply to logarithms with other bases (e.g., base 10), the simplification steps will differ. You would need to utilize the change-of-base formula to convert to a base you can easily work with, often base e or base 10.
Q3: What are some real-world applications of these concepts?
A3: Exponential and logarithmic functions have numerous real-world applications. Some examples include:
- Population growth: Modeling the growth of populations (human, animal, bacterial).
- Radioactive decay: Calculating the decay rate of radioactive materials.
- Compound interest: Determining the future value of an investment with compounding interest.
- Chemical reactions: Analyzing the rate of chemical reactions.
- Signal processing: Analyzing and manipulating signals in various applications (audio, image, etc.).
Q4: What if the expression was more complicated, for example, 2 * e^(ln(3/e))?
A4: The approach remains similar. First simplify the argument of the logarithm (3/e) then apply the logarithm properties to simplify it. Substitute the result back into the expression and finally simplify using the exponential properties. The key is to systematically break down the expression using known properties of logarithms and exponents.
Conclusion: Mastering Logarithms and Exponentials
Understanding the relationship between exponential and logarithmic functions, particularly the natural logarithm and the exponential function with base e, is critical for success in various mathematical and scientific fields. The seemingly simple expression 1 * e^(ln 1/e) serves as an excellent illustration of these fundamental concepts. By breaking down the expression step-by-step, applying relevant properties, and understanding the inverse relationship between the functions, we arrived at a clear and concise solution. This problem underscores the importance of mastering these core mathematical concepts and developing a strong understanding of their practical applications. Further exploration into these topics will undoubtedly lead to a deeper appreciation for their power and elegance in solving complex problems.
Latest Posts
Latest Posts
-
Masks From Romeo And Juliet
Sep 07, 2025
-
Slime With Baking Soda Recipe
Sep 07, 2025
-
165 Degrees F To C
Sep 07, 2025
-
The Rubber People In Nahuatl
Sep 07, 2025
-
What Does G H S Stand For
Sep 07, 2025
Related Post
Thank you for visiting our website which covers about 1 E Ln 1 E . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.