1 3 X 3 3
straightsci
Aug 29, 2025 · 6 min read
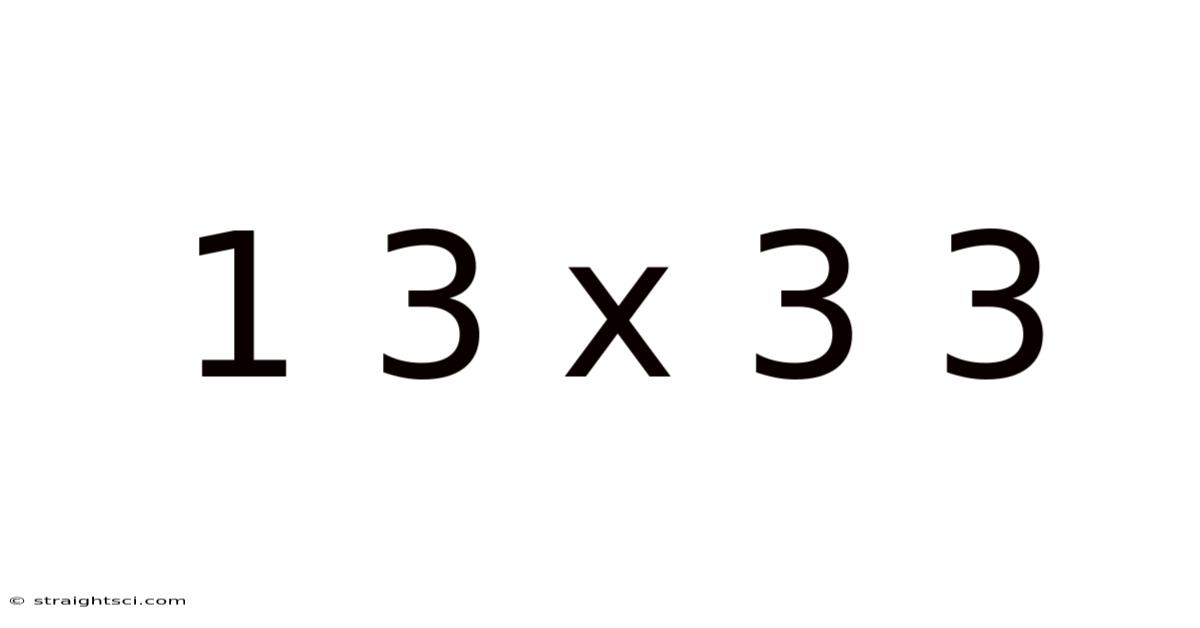
Table of Contents
Decoding the Enigma: A Deep Dive into 1 3 x 3 3
This article explores the mathematical expression "1 3 x 3 3," delving into its various interpretations, potential ambiguities, and the fundamental mathematical principles involved. We'll examine different approaches to solving this expression, highlighting the importance of order of operations (PEMDAS/BODMAS) and exploring related concepts like multiplication, exponentiation, and the significance of clear notation. Understanding this seemingly simple expression reveals crucial insights into the foundations of arithmetic and algebra.
Introduction: The Importance of Order of Operations
At first glance, "1 3 x 3 3" might seem straightforward. However, the lack of explicit operators between the numbers introduces ambiguity. This is where the order of operations, often remembered by the acronyms PEMDAS (Parentheses, Exponents, Multiplication and Division, Addition and Subtraction) or BODMAS (Brackets, Orders, Division and Multiplication, Addition and Subtraction), becomes critical. These mnemonics dictate the sequence in which mathematical operations should be performed to obtain a consistent and unambiguous result. Without adhering to a standardized order, multiple interpretations and potentially incorrect answers can arise. This seemingly simple expression serves as a perfect illustration of why precise mathematical notation is paramount.
Interpretation 1: Implicit Multiplication and Exponentiation
One possible interpretation of "1 3 x 3 3" involves treating the juxtaposed numbers as implicit multiplications and interpreting "3 3" as exponentiation (3 raised to the power of 3). This leads to the following calculation:
- Exponentiation: 3 3 = 3 x 3 x 3 = 27
- Multiplication: 13 x 27 = 351
Therefore, under this interpretation, the solution to "1 3 x 3 3" is 351. This approach relies on the common mathematical convention that adjacent numbers without an explicit operator represent multiplication. Furthermore, it utilizes the understanding that a number immediately followed by another number with no operator implies exponentiation.
Interpretation 2: Implicit Multiplication Only
Another interpretation considers only implicit multiplication between the numbers. This approach might treat the expression as (13) x (33). Here's how the calculation unfolds:
- Multiplication: 13 x 33 = 429
Thus, under this interpretation, the answer to "1 3 x 3 3" is 429. This method highlights the potential for error if we don't clarify the intended operation between the numbers '3' and '3'.
The Crucial Role of Notation: Why Clarity Matters
The discrepancies in the results from the two interpretations above emphasize the paramount importance of precise mathematical notation. Ambiguous expressions can lead to significant errors, especially in more complex calculations. The use of parentheses, brackets, and explicit operators (×, +, -, ÷) removes any uncertainty and ensures a single, unambiguous interpretation.
For instance, to clarify the first interpretation, we could rewrite the expression as "13 x (3^3)" or "13 x 3³". This unambiguous notation leaves no room for misinterpretation. Similarly, the second interpretation could be expressed as "(13) x (33)." Using parentheses makes the intended order of operations clear and eliminates ambiguity.
Expanding the Concept: Exploring Similar Expressions
The principle of order of operations isn't limited to "1 3 x 3 3". It's a fundamental concept that applies to all arithmetic and algebraic manipulations. Let's consider some similar expressions to further illustrate this point:
-
2 4 + 5 2: Applying BODMAS/PEMDAS, we solve the exponentiations first (4² = 16 and 5² = 25), leading to 2 x 16 + 25 = 32 + 25 = 57.
-
10 + 2 x 3 – 1: Following the order of operations, multiplication comes before addition and subtraction. Thus, 10 + 6 – 1 = 15.
-
(4 + 2) x 3²: Parentheses take precedence. 6 x 9 = 54
These examples further demonstrate how the order of operations ensures consistency and accuracy in mathematical computations. Without adhering to this established order, we’d get wildly different and incorrect results.
The Power of Exponentiation: A Deeper Look
The expression "1 3 x 3 3" brings to the forefront the importance of understanding exponentiation, a fundamental mathematical operation. Exponentiation represents repeated multiplication. For example, 3³ (or 3 to the power of 3) signifies 3 multiplied by itself three times (3 x 3 x 3). It's a powerful operation with numerous applications in various fields, including science, engineering, and finance.
Understanding exponential growth is crucial in numerous contexts. Population growth, compound interest calculations, and the spread of diseases often follow exponential patterns. The expression "1 3 x 3 3" might seem simple, but it serves as a gateway to understanding these broader concepts.
Beyond the Numbers: The Essence of Mathematical Rigor
The seemingly simple expression "1 3 x 3 3" highlights a crucial aspect of mathematics: the need for rigorous and unambiguous notation. The absence of clear operators leads to multiple interpretations, underscoring the importance of writing mathematical expressions with precision and clarity. This principle extends beyond simple arithmetic problems; it's fundamental to all branches of mathematics and essential for accurate communication and problem-solving.
The lack of clarity in the original expression can be seen as a thought experiment in the importance of precision in mathematical language. It demonstrates how easily errors can arise from ambiguous notation and reinforces the value of adhering to established mathematical conventions.
Frequently Asked Questions (FAQ)
- Q: What is the correct answer to "1 3 x 3 3"?
A: There's no single "correct" answer without clarifying the intended order of operations. Depending on the interpretation, the answer can be 351 or 429. The best way to avoid ambiguity is to use appropriate notation, such as parentheses or explicit operators.
- Q: Why is order of operations important?
A: Order of operations ensures consistency and eliminates ambiguity in mathematical calculations. Without a standardized order, different people might arrive at different results for the same expression, leading to confusion and errors.
- Q: What are some common mistakes people make when dealing with expressions like this?
A: Common mistakes include performing operations out of order, misinterpreting implicit multiplication, and not using parentheses to clarify the intended order of calculations.
- Q: How can I avoid making these mistakes?
A: Always remember the order of operations (PEMDAS/BODMAS). Use parentheses to clarify the order of calculations, especially when dealing with implicit multiplications or complex expressions. Double-check your work to ensure accuracy.
Conclusion: A Simple Expression, Profound Lessons
The analysis of "1 3 x 3 3" might seem like a trivial exercise, but it reveals fundamental principles crucial to understanding mathematics. The ambiguity inherent in the expression highlights the necessity of precise notation, the importance of order of operations, and the power of exponentiation. These are not merely abstract concepts; they are essential tools for solving problems and understanding the world around us. This exploration emphasizes the significance of clear communication in mathematics, enabling accurate calculations and fostering a deeper appreciation for the beauty and logic of the mathematical world. Remember that clarity in expression is the cornerstone of accurate mathematical understanding. By learning from this seemingly simple problem, we improve our mathematical skills and become better problem-solvers.
Latest Posts
Latest Posts
-
Kalahari Desert Location In Africa
Aug 29, 2025
-
1 76 M Height In Feet
Aug 29, 2025
-
How To Calculate Comparative Advantage
Aug 29, 2025
-
Convert 72 Kg To Lbs
Aug 29, 2025
-
Period Of Rotation For Mars
Aug 29, 2025
Related Post
Thank you for visiting our website which covers about 1 3 X 3 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.