1 3 X 1 4
straightsci
Sep 12, 2025 · 6 min read
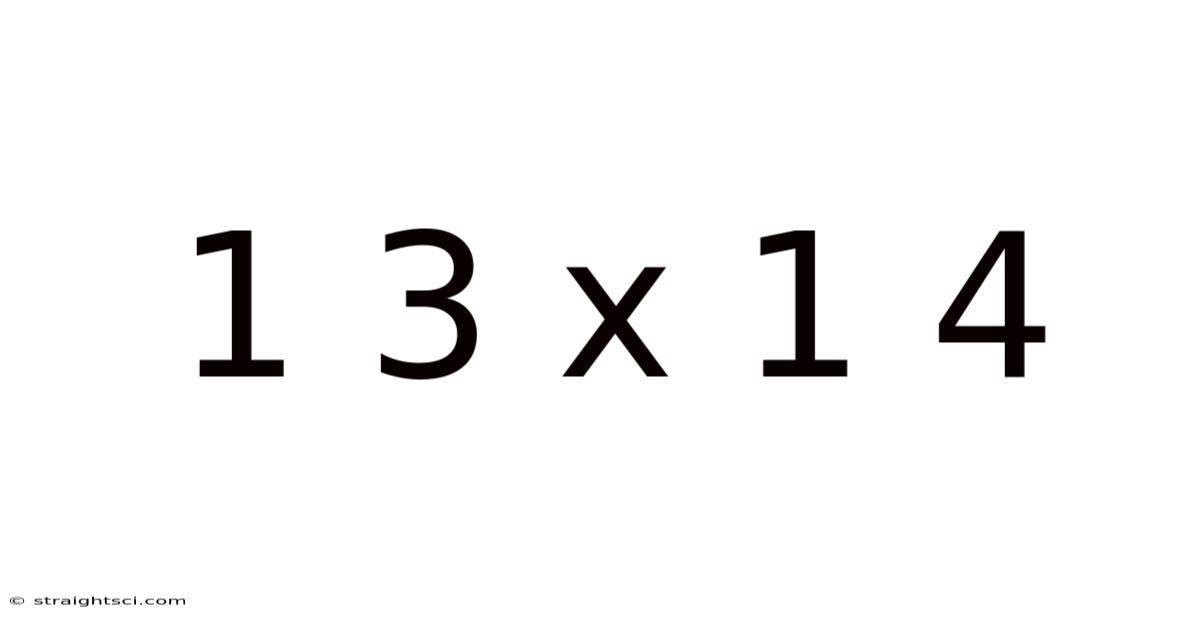
Table of Contents
Decoding 1 3 x 1 4: A Deep Dive into Fraction Multiplication
Understanding fraction multiplication can seem daunting at first, but with a clear approach and some practice, it becomes surprisingly straightforward. This article will guide you through the process of multiplying 1 3/4 by another number, explaining the mechanics, providing examples, exploring the underlying mathematical principles, and addressing common questions. We'll cover various methods, ensuring you master this fundamental mathematical concept. By the end, you'll be confident in tackling any fraction multiplication problem.
Understanding Mixed Numbers and Improper Fractions
Before diving into the multiplication, let's clarify the type of fraction we're dealing with: 1 3/4 is a mixed number. A mixed number combines a whole number (1 in this case) and a proper fraction (3/4). To effectively multiply mixed numbers, it's often easier to convert them into improper fractions. An improper fraction has a numerator (top number) larger than or equal to its denominator (bottom number).
To convert 1 3/4 to an improper fraction:
- Multiply the whole number by the denominator: 1 x 4 = 4
- Add the numerator to the result: 4 + 3 = 7
- Keep the same denominator: 7/4
Therefore, 1 3/4 is equivalent to 7/4. This conversion is crucial for simplifying the multiplication process.
Multiplying Fractions: The Basic Principle
The core principle of fraction multiplication is remarkably simple: multiply the numerators together, and then multiply the denominators together. For example, if we were multiplying 2/3 by 5/7, the calculation would be:
(2 x 5) / (3 x 7) = 10/21
This rule applies regardless of whether the fractions are proper or improper.
Multiplying 1 3/4 by a Whole Number
Let's start with a straightforward example: multiplying 1 3/4 by 2. First, convert 1 3/4 to its improper fraction equivalent, 7/4. Then, we can rewrite the problem as:
(7/4) x 2
To make this easier, we can express the whole number 2 as a fraction: 2/1. Now the multiplication becomes:
(7/4) x (2/1) = (7 x 2) / (4 x 1) = 14/4
The result, 14/4, is an improper fraction. To convert it back to a mixed number:
- Divide the numerator by the denominator: 14 ÷ 4 = 3 with a remainder of 2
- The whole number part of the mixed number is the quotient: 3
- The fraction part has the remainder as the numerator and the original denominator: 2/4
- Simplify the fraction if possible: 2/4 simplifies to 1/2
Therefore, (7/4) x 2 = 14/4 = 3 1/2
Multiplying 1 3/4 by Another Fraction
Let's increase the complexity. Let's multiply 1 3/4 by 2/5. Again, we convert 1 3/4 to 7/4:
(7/4) x (2/5) = (7 x 2) / (4 x 5) = 14/20
This result, 14/20, can be simplified by finding the greatest common divisor (GCD) of 14 and 20, which is 2. Dividing both the numerator and denominator by 2 gives us:
14/20 = 7/10
Therefore, 1 3/4 x 2/5 = 7/10
Multiplying 1 3/4 by a Mixed Number
Multiplying 1 3/4 by another mixed number involves a similar process. Let's try 1 3/4 x 2 1/2. First, convert both mixed numbers to improper fractions:
1 3/4 = 7/4 2 1/2 = 5/2
Now, multiply the improper fractions:
(7/4) x (5/2) = (7 x 5) / (4 x 2) = 35/8
Converting 35/8 back to a mixed number:
35 ÷ 8 = 4 with a remainder of 3
So, 35/8 = 4 3/8
Therefore, 1 3/4 x 2 1/2 = 4 3/8
Cancelling Common Factors (Simplification Before Multiplication)
A useful technique to simplify the calculation is to cancel common factors before multiplying. Let's revisit (7/4) x (2/5). Notice that 2 (the numerator of the second fraction) and 4 (the denominator of the first fraction) share a common factor of 2. We can simplify:
(7/4) x (2/5) = (7/2) x (1/5) = 7/10
This method eliminates the need to simplify the final answer, making the calculation more efficient.
Real-World Applications of Fraction Multiplication
Fraction multiplication isn't just an abstract mathematical concept; it has numerous practical applications in everyday life:
- Cooking and Baking: Scaling recipes up or down often requires multiplying fractions. If a recipe calls for 1 3/4 cups of flour and you want to double it, you'll multiply 1 3/4 by 2.
- Measurement and Construction: In construction or DIY projects, you might need to calculate lengths or areas involving fractions of inches or feet.
- Finance: Calculating discounts, interest, or portions of a budget often involves fraction multiplication.
- Data Analysis: Many statistical calculations use fractions and require multiplication to solve for specific values.
Common Mistakes to Avoid
Several common errors can arise when multiplying fractions:
- Forgetting to convert mixed numbers: Always convert mixed numbers to improper fractions before multiplying.
- Incorrect simplification: Ensure you simplify fractions completely by finding the greatest common divisor.
- Ignoring the order of operations: Remember to follow the order of operations (PEMDAS/BODMAS) if your problem involves other mathematical operations.
Frequently Asked Questions (FAQ)
Q: What if I multiply a fraction by 0?
A: Any fraction multiplied by 0 will always equal 0.
Q: Can I multiply fractions with different denominators?
A: Yes, you absolutely can. The process remains the same: multiply the numerators and multiply the denominators.
Q: Is it always necessary to simplify the final answer?
A: While not strictly mandatory, simplifying the fraction to its lowest terms is considered best practice for clarity and consistency.
Q: How do I multiply more than two fractions?
A: Simply extend the process. Multiply all the numerators together and then multiply all the denominators together. Look for opportunities to cancel common factors before multiplying to simplify the process.
Q: What if the result is an improper fraction?
A: Convert the improper fraction to a mixed number to express the answer in a more understandable format.
Conclusion
Mastering fraction multiplication is a crucial step in developing a strong foundation in mathematics. By understanding the basic principles, practicing regularly, and employing techniques like converting mixed numbers to improper fractions and cancelling common factors, you can confidently tackle even complex problems involving fractions like 1 3/4. Remember to approach each step methodically, and soon, you'll find this once-challenging concept becomes second nature. With consistent practice and a clear understanding of the underlying concepts, you'll build confidence and proficiency in this essential mathematical skill, opening doors to more advanced mathematical explorations. Remember that mathematics is a journey of understanding, and every step forward, no matter how small, contributes to a larger picture of mathematical literacy.
Latest Posts
Latest Posts
-
Where Is Red Bone Marrow
Sep 12, 2025
-
Rough Vs Smooth Endoplasmic Reticulum
Sep 12, 2025
-
Scientific Name Of A Coyote
Sep 12, 2025
-
When Do Frontal Lobes Develop
Sep 12, 2025
-
What Do Race Stand For
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about 1 3 X 1 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.