1 3 Cup X 2
straightsci
Sep 17, 2025 · 6 min read
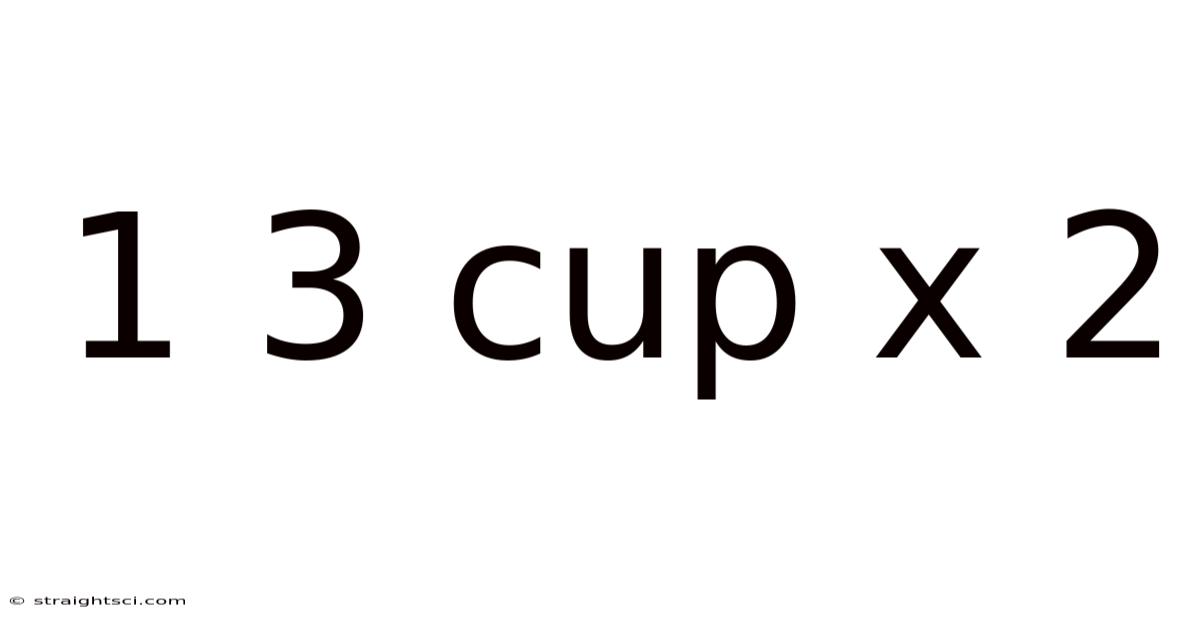
Table of Contents
Decoding 1 3/4 Cups x 2: A Comprehensive Guide to Fraction Multiplication and its Applications
Understanding how to multiply fractions, especially in practical contexts like cooking or crafting, is a crucial life skill. This article delves into the seemingly simple calculation of 1 3/4 cups multiplied by 2, explaining the process step-by-step, exploring the underlying mathematical principles, and highlighting real-world applications where this type of calculation is essential. We'll demystify the process, making it accessible to everyone, regardless of their mathematical background. By the end, you'll not only know the answer but also understand why the answer is what it is.
Introduction: Why Multiplying Fractions Matters
Multiplying fractions might seem like a dry, academic exercise, but it's a fundamental concept with widespread practical use. From doubling recipes in the kitchen to calculating fabric requirements for a sewing project, understanding fraction multiplication allows for accurate measurements and efficient planning. This article uses the example of 1 3/4 cups x 2 to demonstrate the method, but the principles can be applied to any fraction multiplication problem. Mastering this skill ensures accurate results and avoids errors that could impact the outcome of various tasks.
Understanding the Problem: 1 3/4 Cups x 2
The problem "1 3/4 cups x 2" asks us to find the total quantity if we double the amount of 1 3/4 cups. This involves multiplying a mixed number (a number containing both a whole number and a fraction) by a whole number. Let's break down the process into manageable steps.
Step-by-Step Calculation: Transforming and Multiplying
-
Convert the Mixed Number to an Improper Fraction: The first step is to convert the mixed number 1 3/4 into an improper fraction. An improper fraction has a numerator (top number) larger than or equal to its denominator (bottom number). To do this, we multiply the whole number (1) by the denominator (4), add the numerator (3), and keep the same denominator. This gives us:
1 3/4 = (1 x 4 + 3) / 4 = 7/4
-
Multiply the Fractions: Now we can multiply the improper fraction (7/4) by the whole number (2). Remember that a whole number can be written as a fraction with a denominator of 1 (2/1). The multiplication is straightforward:
(7/4) x (2/1) = (7 x 2) / (4 x 1) = 14/4
-
Simplify the Result: The result, 14/4, is an improper fraction. To express it as a mixed number (more easily understood in real-world applications), we divide the numerator (14) by the denominator (4). This gives us a quotient of 3 and a remainder of 2. Therefore:
14/4 = 3 2/4
-
Reduce the Fraction (if necessary): Finally, we simplify the fraction part of the mixed number. Both 2 and 4 are divisible by 2, so we can simplify 2/4 to 1/2. Therefore, our final answer is:
3 2/4 = 3 1/2
Therefore, 1 3/4 cups x 2 = 3 1/2 cups.
Alternative Method: Distributive Property
Another approach to solving this problem involves using the distributive property. This method is particularly useful when working with larger mixed numbers. We can break down the problem like this:
-
Separate the Whole Number and Fraction: Rewrite 1 3/4 as 1 + 3/4.
-
Apply the Distributive Property: Multiply each part separately by 2:
2 * (1 + 3/4) = (2 * 1) + (2 * 3/4) = 2 + 6/4
-
Simplify: Simplify 6/4 to 1 2/4, then further reduce it to 1 1/2.
-
Combine: Add the results: 2 + 1 1/2 = 3 1/2 cups.
This method showcases a different mathematical approach to reach the same correct answer.
The Science Behind Fraction Multiplication: Why It Works
The underlying principle behind fraction multiplication is the concept of repeated addition and the representation of fractions as parts of a whole. Multiplying 1 3/4 by 2 means adding 1 3/4 to itself. Visualizing this can be helpful: imagine two measuring cups, each filled to the 1 3/4 mark. Combining the contents of both cups will clearly result in 3 1/2 cups. This visual representation reinforces the mathematical process.
Real-World Applications: Beyond the Classroom
The ability to multiply fractions isn't just a classroom skill; it's essential in numerous everyday situations:
-
Cooking and Baking: Doubling or tripling recipes requires accurate fraction multiplication. Incorrect calculations can significantly alter the taste and texture of the final dish.
-
Sewing and Crafting: Calculating fabric requirements, yarn lengths, or bead counts often involves fractional measurements. Accurate calculations prevent material shortages and ensure project success.
-
Construction and DIY: Measuring materials like wood, concrete, or paint frequently involves fractions. Precise calculations are vital for achieving accurate dimensions and avoiding costly mistakes.
-
Financial Calculations: Understanding fractions is vital for calculating percentages, discounts, and interest rates—all crucial for managing personal finances.
-
Science and Engineering: Fractions are ubiquitous in scientific and engineering applications. They are crucial in calculations involving proportions, ratios, and measurements.
Frequently Asked Questions (FAQ)
-
Q: What if I have to multiply by a fraction instead of a whole number? A: The process remains the same. Simply multiply the numerators together and the denominators together, then simplify the resulting fraction.
-
Q: How do I multiply mixed numbers with different denominators? A: Convert both mixed numbers to improper fractions, find a common denominator, and then multiply as before.
-
Q: Are there any online calculators or tools that can help? A: While many online calculators can perform fraction multiplication, understanding the underlying process is far more valuable than relying solely on tools. The goal should be to internalize the method, allowing for independent problem-solving in different situations.
-
Q: Why is it important to simplify the fraction at the end? A: Simplifying fractions provides the most concise and easily understandable representation of the answer. It's essential for clarity and accuracy, especially in practical applications.
Conclusion: Mastering Fraction Multiplication for a Brighter Future
Mastering fraction multiplication is a significant step towards greater mathematical proficiency and enhances problem-solving skills in various everyday contexts. While initially challenging, understanding the step-by-step process, employing different methods like the distributive property, and recognizing the underlying mathematical principles, empowers individuals to confidently tackle fraction calculations. This skill translates to improved accuracy and efficiency in various fields, making it a valuable asset throughout life. The seemingly simple problem of 1 3/4 cups x 2 provides a gateway to understanding a far broader range of mathematical concepts and practical applications, laying a strong foundation for future learning and problem-solving. So, embrace the challenge, practice regularly, and unlock the power of fraction multiplication!
Latest Posts
Latest Posts
-
And I Took That Personally
Sep 17, 2025
-
What Is A Crystal Lattice
Sep 17, 2025
-
Number Of Electrons For Aluminum
Sep 17, 2025
-
Bohr Rutherford Diagram Of Boron
Sep 17, 2025
-
Periodic Table Liquid Gas Solid
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 1 3 Cup X 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.