1 20 As A Percent
straightsci
Aug 27, 2025 · 5 min read
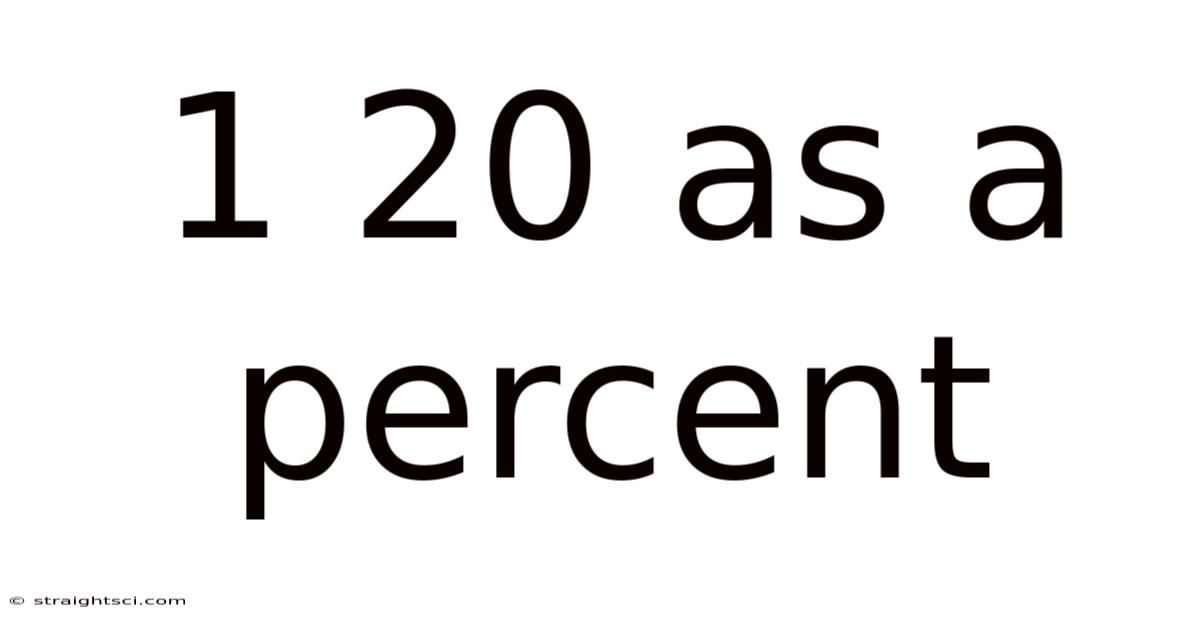
Table of Contents
Understanding 1/20 as a Percentage: A Comprehensive Guide
What is 1/20 as a percentage? This seemingly simple question opens the door to understanding fundamental concepts in mathematics, particularly fractions, decimals, and percentages – concepts crucial for everyday life, from calculating discounts to understanding financial reports. This article will delve deep into how to convert 1/20 to a percentage, explore the underlying principles, and offer practical applications to solidify your understanding.
Introduction: Fractions, Decimals, and Percentages
Before diving into the specific conversion of 1/20, let's refresh our understanding of the three key players: fractions, decimals, and percentages.
-
Fractions: Represent a part of a whole. They consist of a numerator (the top number) and a denominator (the bottom number). For example, in the fraction 1/20, 1 is the numerator and 20 is the denominator. This signifies one part out of a total of twenty equal parts.
-
Decimals: Represent numbers less than one using a base-ten system. They are expressed using a decimal point, separating the whole number part from the fractional part. For example, 0.5 represents one-half.
-
Percentages: Represent a fraction or decimal as a portion of 100. The symbol "%" signifies "per hundred". For instance, 50% means 50 out of 100, or one-half.
The ability to convert between these three forms is essential for various mathematical operations and real-world problem-solving.
Converting 1/20 to a Percentage: Step-by-Step Guide
Converting 1/20 to a percentage involves two main steps:
Step 1: Convert the Fraction to a Decimal
To convert a fraction to a decimal, we divide the numerator by the denominator:
1 ÷ 20 = 0.05
Therefore, 1/20 as a decimal is 0.05.
Step 2: Convert the Decimal to a Percentage
To convert a decimal to a percentage, we multiply the decimal by 100 and add the "%" symbol:
0.05 × 100 = 5%
Therefore, 1/20 as a percentage is 5%.
Illustrative Examples: Real-World Applications
Let's solidify our understanding with some real-world examples where understanding 1/20 as 5% is crucial:
-
Discounts: A store offers a 5% discount on all items. If an item costs $100, the discount would be 5% of $100, which is (5/100) * $100 = $5. This is the same as calculating (1/20) * $100 = $5.
-
Taxes: A sales tax rate is 5%. If you buy an item for $200, the tax amount would be 5% of $200, or $10. Again, this is equivalent to calculating (1/20) * $200 = $10.
-
Surveys and Statistics: In a survey of 20 people, if only one person prefers a particular option, that represents 1/20 or 5% of the total respondents.
-
Financial Calculations: Understanding percentages is vital in finance. For example, calculating interest rates, returns on investments, or analyzing financial statements often involves converting fractions or decimals to percentages. A 5% interest rate on a loan means you pay 5% of the principal amount as interest.
-
Proportions and Ratios: The fraction 1/20 represents a ratio of 1:19. This ratio can be used to represent various proportions in various fields, such as mixing ingredients, analyzing data, or scaling models.
Further Exploration: Extending the Concept
Understanding 1/20 as 5% opens doors to more complex percentage calculations. For example:
-
Calculating percentages of larger numbers: If we want to find 5% of 500, we can use the fraction 1/20: (1/20) * 500 = 25.
-
Working backward from a percentage: If we know that 5% of a number is 10, we can find the original number by multiplying 10 by 20 (since 5% is 1/20): 10 * 20 = 200.
Mathematical Explanation: Why it Works
The conversion from a fraction to a percentage relies on the fundamental concept that a percentage is simply a fraction with a denominator of 100.
To convert any fraction to a percentage, you follow these steps:
-
Divide the numerator by the denominator. This gives you the decimal equivalent of the fraction.
-
Multiply the decimal by 100. This scales the decimal to express it as a part of 100, thus giving you the percentage.
In our case of 1/20:
-
1 ÷ 20 = 0.05
-
0.05 × 100 = 5%
This method works because multiplying by 100 is equivalent to multiplying by (100/1), which can be seen as a conversion factor transforming the fraction from its original denominator to a denominator of 100.
Frequently Asked Questions (FAQ)
Q: Can I convert 1/20 to a percentage using a different method?
A: Yes, you can. Another approach is to find an equivalent fraction with a denominator of 100. Since 20 multiplied by 5 equals 100, we multiply both the numerator and the denominator of 1/20 by 5: (15)/(205) = 5/100. This directly translates to 5%.
Q: What if the fraction doesn't easily convert to a denominator of 100?
A: If the denominator doesn't have 100 as a multiple, you still use the division method (numerator divided by denominator) followed by multiplication by 100 to obtain the percentage.
Q: Are there any online tools or calculators to help with percentage conversions?
A: Yes, many online calculators can perform fraction-to-percentage conversions quickly and efficiently. However, understanding the underlying mathematical principles is more important than relying solely on calculators.
Q: Why is understanding percentages important?
A: Percentages are a fundamental part of daily life, used in various contexts like finance, shopping, statistics, and more. They provide a standardized way to compare proportions and understand relative quantities.
Conclusion: Mastering Percentage Conversions
Understanding how to convert 1/20 to a percentage, and more generally, how to work with fractions, decimals, and percentages, is a vital skill applicable to numerous areas of life. This article not only provides a step-by-step guide but also delves into the underlying mathematical principles and showcases real-world applications. By mastering these concepts, you enhance your mathematical abilities and gain a deeper understanding of the world around you. Remember that consistent practice and applying these concepts in various scenarios are key to achieving proficiency. Don't hesitate to explore further examples and practice converting different fractions and decimals into percentages to further strengthen your understanding.
Latest Posts
Latest Posts
-
Subtracting Exponents With Like Bases
Aug 27, 2025
-
Where Is The Tibia Located
Aug 27, 2025
-
73 Kg How Many Pounds
Aug 27, 2025
-
Is Canada A Mixed Economy
Aug 27, 2025
-
53 Kg How Many Pounds
Aug 27, 2025
Related Post
Thank you for visiting our website which covers about 1 20 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.