1 2 X 1 3
straightsci
Sep 15, 2025 · 5 min read
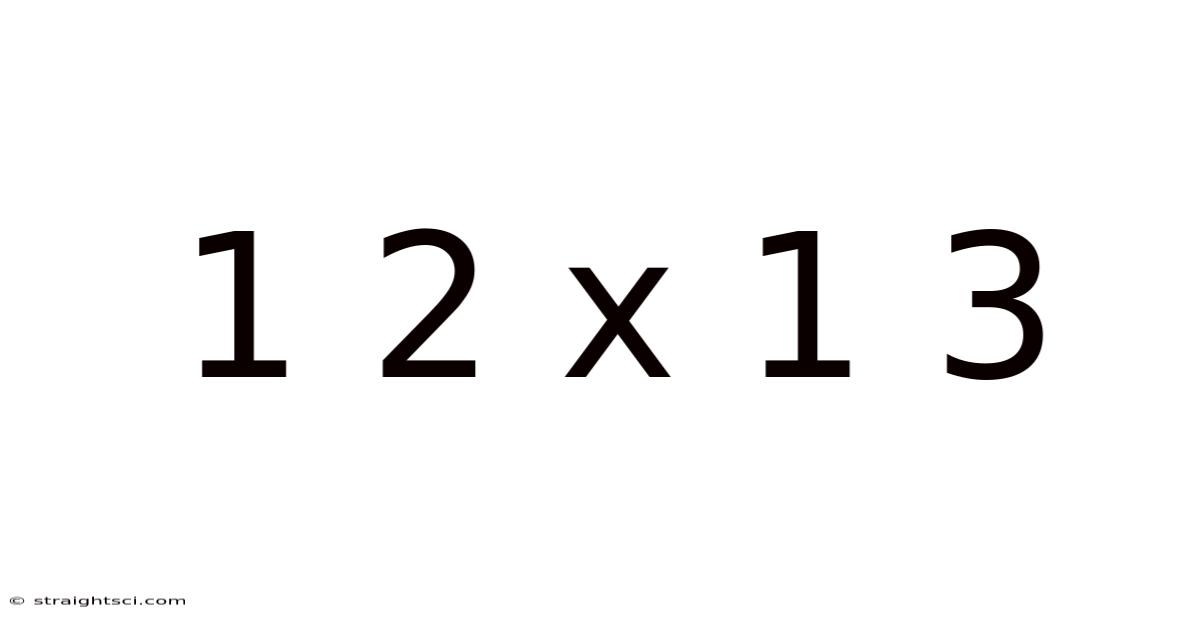
Table of Contents
Decoding 1 2 x 1 3: A Deep Dive into Multiplication and Beyond
This article explores the seemingly simple mathematical equation "1 2 x 1 3," delving far beyond the basic arithmetic to uncover the underlying principles, applications, and broader mathematical concepts it represents. We'll dissect the process of multiplication, examine its significance in various fields, and even venture into related areas like algebra and advanced mathematics. This is more than just solving a simple equation; it's about understanding the building blocks of mathematical reasoning.
Introduction: The Fundamentals of Multiplication
At its core, "1 2 x 1 3" represents a multiplication problem. Multiplication is a fundamental arithmetic operation that essentially involves repeated addition. In this case, we're multiplying 12 by 13. This means adding 12 to itself 13 times, or vice-versa. The result is the product of the two numbers. While the calculation itself is straightforward, understanding the underlying concept of repeated addition is crucial for grasping more advanced mathematical ideas. The solution to 12 x 13 is 156. But let's not stop there. This seemingly simple equation opens doors to a much wider world of mathematical concepts.
Step-by-Step Calculation: Breaking Down 12 x 13
Let's illustrate the calculation using two common methods:
1. Standard Multiplication Algorithm:
This method involves breaking down the numbers into their place values (tens and ones) and performing multiplication systematically:
12
x 13
------
36 (12 x 3)
120 (12 x 10)
------
156 (Sum of partial products)
This demonstrates the distributive property of multiplication over addition: 12 x 13 = 12 x (10 + 3) = (12 x 10) + (12 x 3) = 120 + 36 = 156.
2. Lattice Multiplication:
This less common but visually intuitive method uses a grid to organize the multiplication process:
1 | 2
-------+-------
1 | 1 | 2
3 | 3 | 6
-------+-------
1 | 5 | 6
Each small square represents the product of a digit from the multiplicand (12) and a digit from the multiplier (13). The diagonal sums give the final product (156).
Beyond the Basics: Exploring Related Mathematical Concepts
The simple calculation 12 x 13 provides a springboard to explore more sophisticated mathematical ideas:
1. Prime Factorization:
Understanding prime numbers is fundamental in number theory. Both 12 and 13 can be broken down into their prime factors:
- 12 = 2 x 2 x 3 (2² x 3)
- 13 = 13 (a prime number itself)
This factorization helps in various mathematical applications, including simplifying fractions and understanding divisibility rules.
2. Algebraic Representation:
We can represent this multiplication problem algebraically. Let's say:
- x = 12
- y = 13
Then the equation becomes: x * y = z, where z is the product (156). This simple algebraic representation opens the door to solving more complex equations involving variables.
3. Modular Arithmetic:
Modular arithmetic deals with remainders after division. For instance, 156 divided by 10 leaves a remainder of 6. This concept is essential in cryptography and other areas of computer science.
4. Number Theory:
The properties of 12 and 13, such as their divisibility, factors, and relationship to other numbers, are explored within number theory. For example, 12 is a composite number (not prime), while 13 is a prime number. This difference has significant implications in various mathematical fields.
5. Applications in Geometry:
Imagine a rectangle with sides measuring 12 units and 13 units. The area of this rectangle would be 12 x 13 = 156 square units. This illustrates the application of multiplication in calculating areas and volumes in geometry.
6. Real-world Applications:
Multiplication is ubiquitous in everyday life. From calculating the cost of multiple items (12 items at $13 each) to determining distances or quantities, understanding multiplication is essential for various practical tasks.
Frequently Asked Questions (FAQs)
Q1: What are some different ways to multiply 12 and 13?
A1: Besides the standard and lattice methods, you can use:
- Distributive property: Break down 13 into 10 and 3, then multiply 12 by each part and add the results.
- Mental math techniques: Some individuals develop strategies to multiply numbers quickly in their heads.
- Using a calculator: This is a convenient method, especially for larger numbers.
Q2: What if the numbers were larger? How would the process change?
A2: The standard algorithm remains the same, though the calculation will involve more steps. For very large numbers, algorithms optimized for speed and efficiency (like those used in computers) are used.
Q3: Is there a limit to how large the numbers can be in a multiplication problem?
A3: No, there's no theoretical limit. Numbers can be arbitrarily large, though practical limitations exist in terms of the time and resources needed for computation.
Q4: Why is understanding multiplication important?
A4: Multiplication is a fundamental building block of mathematics. It's crucial for many areas, including algebra, calculus, physics, engineering, finance, and computer science. It's also essential for everyday tasks and problem-solving.
Q5: Are there any shortcuts or tricks for multiplying numbers quickly?
A5: Many mental math tricks exist, such as multiplying by powers of 10, using the distributive property creatively, or exploiting patterns and relationships between numbers. Practice and familiarity with these techniques improve speed and accuracy.
Conclusion: The Enduring Significance of 12 x 13
The seemingly simple equation "12 x 13" serves as a gateway to a rich world of mathematical concepts and applications. From the basic principles of repeated addition to advanced topics in number theory and algebra, this seemingly simple calculation underscores the interconnectedness of mathematical ideas and the importance of understanding fundamental operations. Its relevance extends far beyond the realm of abstract mathematics, finding applications in diverse fields and impacting our daily lives in countless ways. Mastering multiplication is not just about getting the right answer; it’s about developing a deeper understanding of the logical structures that underpin mathematical reasoning and problem-solving. This foundational knowledge empowers us to tackle increasingly complex challenges and fosters a more profound appreciation for the beauty and power of mathematics. The seemingly simple "12 x 13 = 156" is much more than just a calculation; it's a stepping stone towards a broader understanding of the mathematical universe.
Latest Posts
Latest Posts
-
Km To Miles Conversion Formula
Sep 15, 2025
-
Is 3 6 Equivalent To 1 2
Sep 15, 2025
-
Scientific Name Of The Wolf
Sep 15, 2025
-
Commutative Property And Associative Property
Sep 15, 2025
-
Coral Reef Biome Food Web
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about 1 2 X 1 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.