1/2 X 1/2 X 1/4
straightsci
Sep 10, 2025 · 7 min read
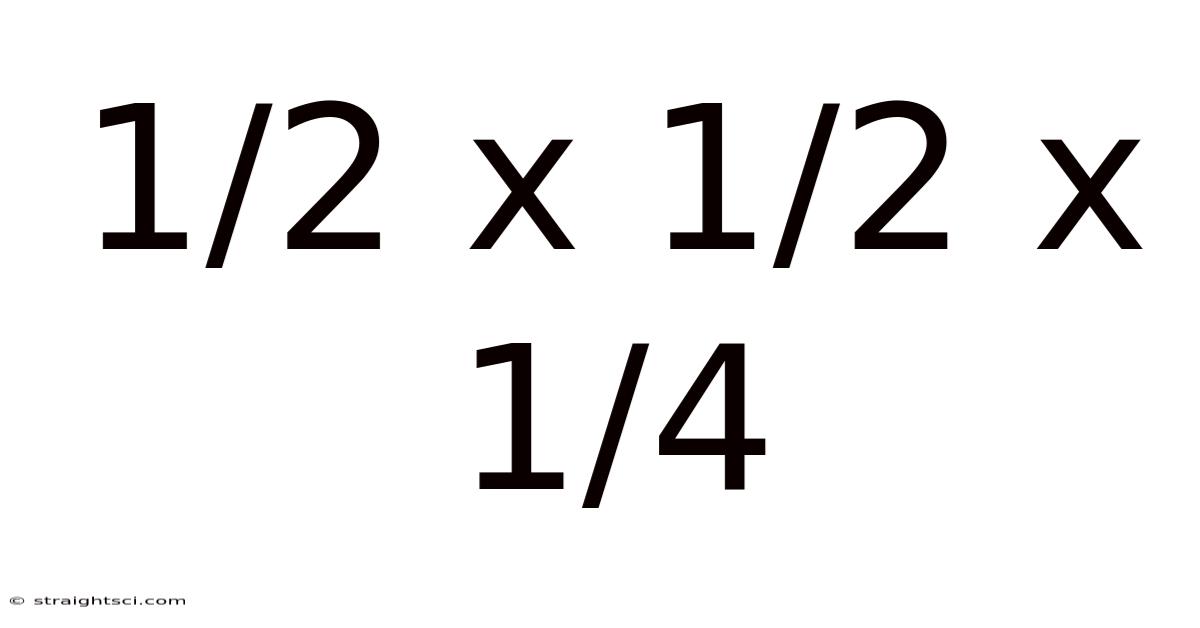
Table of Contents
Decoding 1/2 x 1/2 x 1/4: A Deep Dive into Fraction Multiplication
This article will explore the seemingly simple calculation of 1/2 x 1/2 x 1/4, unraveling the underlying principles of fraction multiplication and extending the understanding to broader applications. We’ll cover the step-by-step process, delve into the mathematical reasoning, and address frequently asked questions. This exploration goes beyond a simple numerical answer; it aims to build a solid foundation in fraction manipulation and its real-world relevance.
Introduction: Understanding Fraction Multiplication
Fractions represent parts of a whole. Multiplying fractions involves finding a portion of a portion. In the case of 1/2 x 1/2 x 1/4, we're finding one-fourth of one-half of one-half. This might seem abstract, but understanding the process is crucial for various mathematical operations and real-world applications, from baking to construction.
Step-by-Step Calculation of 1/2 x 1/2 x 1/4
The simplest approach to multiplying fractions is to multiply the numerators (top numbers) together and then multiply the denominators (bottom numbers) together. Let's break down the calculation:
-
Multiply the numerators: 1 x 1 x 1 = 1
-
Multiply the denominators: 2 x 2 x 4 = 16
-
Combine the results: The final answer is 1/16.
Therefore, 1/2 x 1/2 x 1/4 = 1/16.
Visualizing the Multiplication: A Geometric Approach
Imagine a square representing a whole unit (1). Dividing this square in half horizontally gives you two equal rectangles, each representing 1/2. Now, take one of these 1/2 rectangles and divide it in half vertically. You now have four smaller squares, each representing 1/4 of the original 1/2, or 1/8 of the whole square. Finally, consider one of these 1/8 squares and divide it into four equal parts. Each of these tiny squares represents 1/4 of the 1/8 square, which is 1/32 of the whole square. This visual representation helps to solidify the concept of multiplying fractions as successive divisions.
However, the problem is 1/2 x 1/2 x 1/4, not 1/2 x 1/2 x 1/8. The geometric approach still works but in a slightly different way. Visualize a cube. Divide the cube into two equal halves vertically. Now take one half and divide it into two equal halves horizontally. This will give you 4 equal sized smaller cubes representing 1/4 of the original cube. Now take one of these smaller cubes and cut it into 4 slices along a third dimension (depth). Now we have 16 smaller cubes. One of these cubes is 1/16 of the original cube. This representation visually shows that 1/2 x 1/2 x 1/4 = 1/16
The Mathematical Reasoning Behind Fraction Multiplication
The process of multiplying fractions relies on the commutative and associative properties of multiplication. The commutative property states that the order of multiplication doesn't affect the result (a x b = b x a). The associative property allows us to group numbers in different ways without changing the outcome ((a x b) x c = a x (b x c)). These properties allow us to rearrange and simplify the calculation before performing the multiplication.
For example, we could rewrite 1/2 x 1/2 x 1/4 as (1/2 x 1/2) x 1/4, then calculate 1/4 x 1/4 = 1/16. This demonstrates the flexibility and efficiency inherent in understanding the fundamental properties of multiplication.
Extending the Concept: Multiplying Fractions with Whole Numbers
Understanding fraction multiplication extends to scenarios involving whole numbers. A whole number can be represented as a fraction with a denominator of 1. For instance, 3 can be written as 3/1. Multiplying a fraction by a whole number follows the same principle: multiply the numerators and then the denominators.
For example: 3 x 1/2 = (3/1) x (1/2) = 3/2 = 1 1/2. This shows that multiplying a fraction by a whole number effectively scales the fraction.
Real-World Applications of Fraction Multiplication
Fraction multiplication isn't confined to the realm of abstract mathematics. It finds practical application in numerous real-world situations:
-
Cooking and Baking: Recipes often require fractional amounts of ingredients. Scaling a recipe up or down requires multiplying fractions. For example, if a recipe calls for 1/2 cup of sugar and you want to make double the batch, you'd multiply 1/2 by 2 (2/1), resulting in 1 cup of sugar.
-
Construction and Engineering: Calculating dimensions, material quantities, and proportions in construction and engineering frequently involves fractions and their multiplication.
-
Finance: Calculating percentages, interest rates, and discounts often involves multiplying fractions.
-
Data Analysis: In statistics and data analysis, manipulating and interpreting fractional data requires a strong understanding of fraction multiplication.
Simplifying Fractions: A Crucial Step
After multiplying fractions, it's crucial to simplify the resulting fraction to its lowest terms. This means finding the greatest common divisor (GCD) of the numerator and denominator and dividing both by the GCD. In the case of 1/16, the fraction is already in its simplest form because 1 and 16 share no common divisors other than 1.
Dealing with Mixed Numbers
Mixed numbers (numbers containing both whole and fractional parts, such as 2 1/2) require an extra step before multiplying. First, convert the mixed number into an improper fraction (where the numerator is larger than the denominator). To convert 2 1/2 to an improper fraction:
-
Multiply the whole number by the denominator: 2 x 2 = 4
-
Add the numerator: 4 + 1 = 5
-
Keep the same denominator: 5/2
Now you can perform the multiplication as you would with other fractions.
Frequently Asked Questions (FAQ)
-
Q: What if the fractions have different denominators?
A: Before multiplying, you need to find a common denominator for all fractions involved. This allows you to perform the multiplication smoothly. For example, if you have 1/2 and 1/3, you'd find the least common multiple (LCM) of 2 and 3, which is 6. Then, convert the fractions to have a denominator of 6: 3/6 and 2/6. Now you can multiply: (3/6) x (2/6) = 6/36 = 1/6
-
Q: Can I use a calculator to multiply fractions?
A: Yes, most scientific calculators and online calculators can handle fraction multiplication. However, understanding the manual process is crucial for grasping the underlying mathematical concepts.
-
Q: Are there any shortcuts for multiplying fractions?
A: Yes, you can sometimes simplify before multiplying. If a numerator and a denominator share a common factor, you can cancel them out before proceeding with the multiplication. This can simplify the calculation and reduce the need for simplification later.
-
Q: What happens if one of the fractions is zero?
A: If any of the fractions involved in the multiplication is zero, the entire product will be zero. This is because any number multiplied by zero is always zero.
Conclusion: Mastering Fraction Multiplication
Mastering fraction multiplication is a cornerstone of mathematical proficiency. It's not simply about obtaining the correct numerical answer (in this case, 1/16); it's about understanding the underlying principles, visualizing the process, and appreciating its broad applicability in various fields. By developing a strong foundation in fraction manipulation, you equip yourself with a powerful tool for tackling complex mathematical problems and real-world challenges. The seemingly simple calculation of 1/2 x 1/2 x 1/4 provides a gateway to a deeper understanding of a fundamental mathematical concept with far-reaching implications. Remember to practice regularly and utilize visual aids to strengthen your understanding and build confidence in your ability to tackle more complex fraction operations in the future.
Latest Posts
Latest Posts
-
Sites For Ticket Sales Gamificationsummit
Sep 10, 2025
-
Latitude Of Tropic Of Cancer
Sep 10, 2025
-
Is 4 A Prime Number
Sep 10, 2025
-
Exercises In Present Perfect Tense
Sep 10, 2025
-
Pi Is A Irrational Number
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about 1/2 X 1/2 X 1/4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.