1/2 Of 2 3/4 Cup
straightsci
Sep 24, 2025 · 5 min read
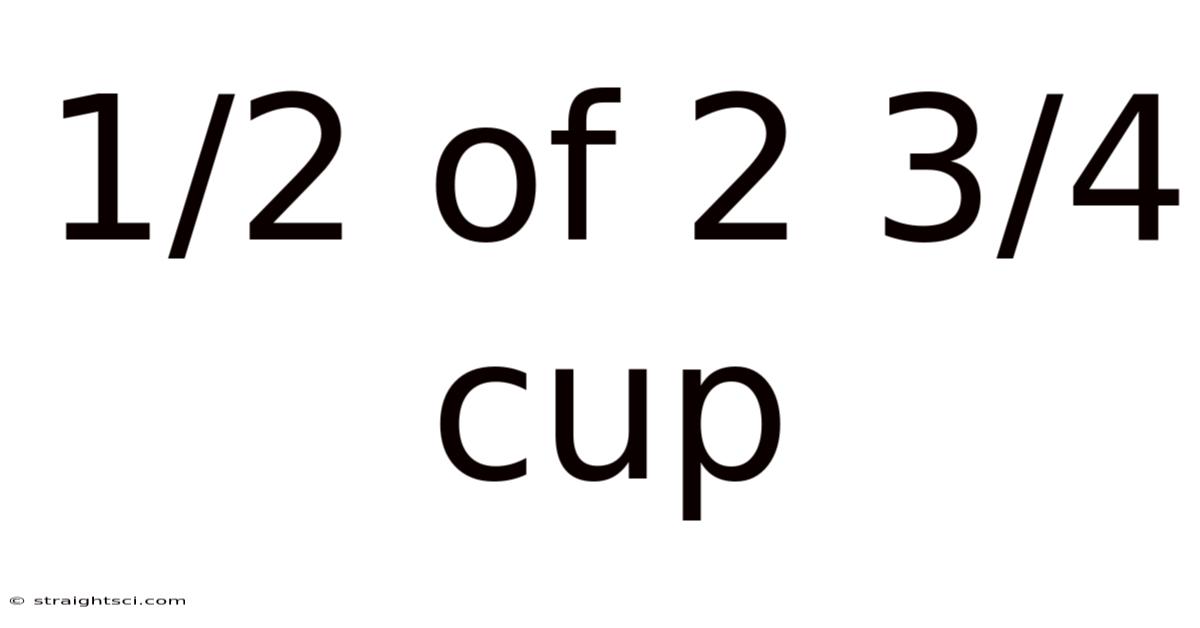
Table of Contents
Decoding Fractions: What is 1/2 of 2 3/4 Cups? A Comprehensive Guide
Understanding fractions is a fundamental skill, essential for everything from baking to advanced mathematics. This article will delve into calculating half of 2 ¾ cups, providing a step-by-step guide suitable for all levels, from beginners struggling with fractions to those seeking a refresher. We'll explore various methods, explain the underlying mathematical principles, and even tackle some frequently asked questions. By the end, you'll not only know the answer but also possess a deeper understanding of fractional arithmetic. This guide is perfect for anyone searching for "half of 2 3/4 cups," "fraction calculation," or "how to divide fractions."
Understanding the Problem: 1/2 of 2 3/4 Cups
The problem asks us to find half of 2 ¾ cups. In mathematical terms, this translates to calculating ½ * 2 ¾. This seemingly simple problem requires a solid grasp of fraction multiplication and conversion. We'll explore several approaches to solve this, highlighting the advantages and disadvantages of each method.
Method 1: Converting to Improper Fractions
This method is often preferred for its mathematical precision and clarity. It involves converting the mixed fraction (2 ¾) into an improper fraction before performing the multiplication.
Step 1: Convert the Mixed Fraction to an Improper Fraction
A mixed fraction (a whole number and a fraction) consists of a whole number part and a fractional part. To convert 2 ¾ to an improper fraction, we multiply the whole number (2) by the denominator (4), add the numerator (3), and keep the same denominator (4).
2 ¾ = (2 * 4 + 3) / 4 = 11/4
Step 2: Perform the Multiplication
Now we can multiply the two fractions:
½ * 11/4 = (1 * 11) / (2 * 4) = 11/8
Step 3: Convert the Improper Fraction Back to a Mixed Fraction (Optional)
The result, 11/8, is an improper fraction (the numerator is larger than the denominator). To express this as a mixed fraction, we divide the numerator (11) by the denominator (8).
11 ÷ 8 = 1 with a remainder of 3
Therefore, 11/8 is equivalent to 1 ¾.
Conclusion (Method 1): Half of 2 ¾ cups is 1 ¾ cups.
Method 2: Working with Whole Numbers and Fractions Separately
This method offers a more intuitive approach, particularly helpful for beginners. It involves separately calculating half of the whole number part and half of the fractional part.
Step 1: Find Half of the Whole Number
Half of 2 cups is simply 2 / 2 = 1 cup.
Step 2: Find Half of the Fractional Part
Half of ¾ cup is (1/2) * (3/4) = 3/8 cup.
Step 3: Combine the Results
Add the results from steps 1 and 2:
1 cup + 3/8 cup = 1 ¾ cups.
Conclusion (Method 2): This method confirms that half of 2 ¾ cups is 1 ¾ cups.
Method 3: Using Decimal Conversion
This method involves converting the mixed fraction to a decimal, performing the calculation, and then converting the result back to a fraction if needed.
Step 1: Convert the Mixed Fraction to a Decimal
2 ¾ can be written as 2 + ¾. Since ¾ = 0.75, 2 ¾ = 2.75
Step 2: Perform the Multiplication
Multiply 2.75 by 0.5 (which is ½):
2.75 * 0.5 = 1.375
Step 3: Convert the Decimal Back to a Fraction (Optional)
To convert 1.375 to a fraction, we can express it as 1 + 0.375. 0.375 can be represented as 375/1000, which simplifies to 3/8. Therefore, 1.375 = 1 3/8 = 1 ¾
Conclusion (Method 3): Again, this confirms that half of 2 ¾ cups is 1 ¾ cups.
Why Different Methods Yield the Same Result: A Mathematical Explanation
All three methods demonstrate different approaches to the same fundamental mathematical operation – multiplication of fractions. The underlying principles remain consistent: we are essentially dividing 2 ¾ by 2. The choice of method depends on personal preference and mathematical comfort. The improper fraction method offers a structured approach, while the separate calculation method leverages intuitive understanding. The decimal conversion method is useful when working with measuring instruments or calculations involving decimal numbers.
Practical Applications and Real-World Examples
Understanding fractional calculations has numerous practical applications in daily life. Beyond baking (where accurately measuring ingredients is crucial), these skills are valuable in:
- Cooking: Scaling recipes up or down requires fractional understanding.
- Sewing: Calculating fabric requirements for projects often involves fractions.
- Construction: Measuring materials and determining quantities necessitates precise fractional arithmetic.
- Finance: Calculating percentages, interest rates, and proportions involves similar principles.
Understanding how to solve problems like "1/2 of 2 3/4 cups" builds a stronger foundation for more complex mathematical concepts.
Frequently Asked Questions (FAQ)
Q1: Can I use a calculator to solve this?
A1: Yes, most calculators can handle fractions. However, understanding the underlying methods is crucial for developing mathematical fluency and problem-solving skills.
Q2: What if the fraction was more complex, like 1/3 of 2 3/4 cups?
A2: The same principles apply. You would convert the mixed fraction to an improper fraction, perform the multiplication, and then simplify the result. For example: (1/3) * (11/4) = 11/12 cups.
Q3: Why is it important to learn fractions?
A3: Fractions are fundamental to many areas of mathematics and science. Mastering fractions builds a solid foundation for algebra, calculus, and other advanced mathematical concepts. They are also essential for everyday tasks and problem-solving in various fields.
Q4: What if I don't have a measuring cup that accurately measures 3/8 of a cup?
A4: You can use a smaller measuring cup or spoon to approximate 3/8 of a cup. Alternatively, you could use a liquid measuring cup and estimate the volume. For baking, especially, precision is vital, so investing in a set of accurate measuring cups is advisable.
Conclusion
Calculating half of 2 ¾ cups, or solving any fractional problem, requires a methodical approach. This article demonstrated three methods, each offering a unique perspective on solving the problem. Whether you prefer the structured approach of improper fractions, the intuitive separation of whole and fractional parts, or the convenience of decimal conversion, the result remains the same: half of 2 ¾ cups is 1 ¾ cups. The ability to confidently tackle such problems strengthens your mathematical skills and equips you to tackle more complex challenges in various aspects of life. Remember that practice is key to mastering fractions, so keep exploring and solving different fractional problems to solidify your understanding.
Latest Posts
Latest Posts
-
Intensive Farming Vs Extensive Farming
Sep 24, 2025
-
Lateral Area Of The Cone
Sep 24, 2025
-
3 4 Cup In Ounces
Sep 24, 2025
-
16 Pounds How Many Ounces
Sep 24, 2025
-
Formula For Frequency In Physics
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about 1/2 Of 2 3/4 Cup . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.