1 2 3 X 3
straightsci
Sep 03, 2025 · 6 min read
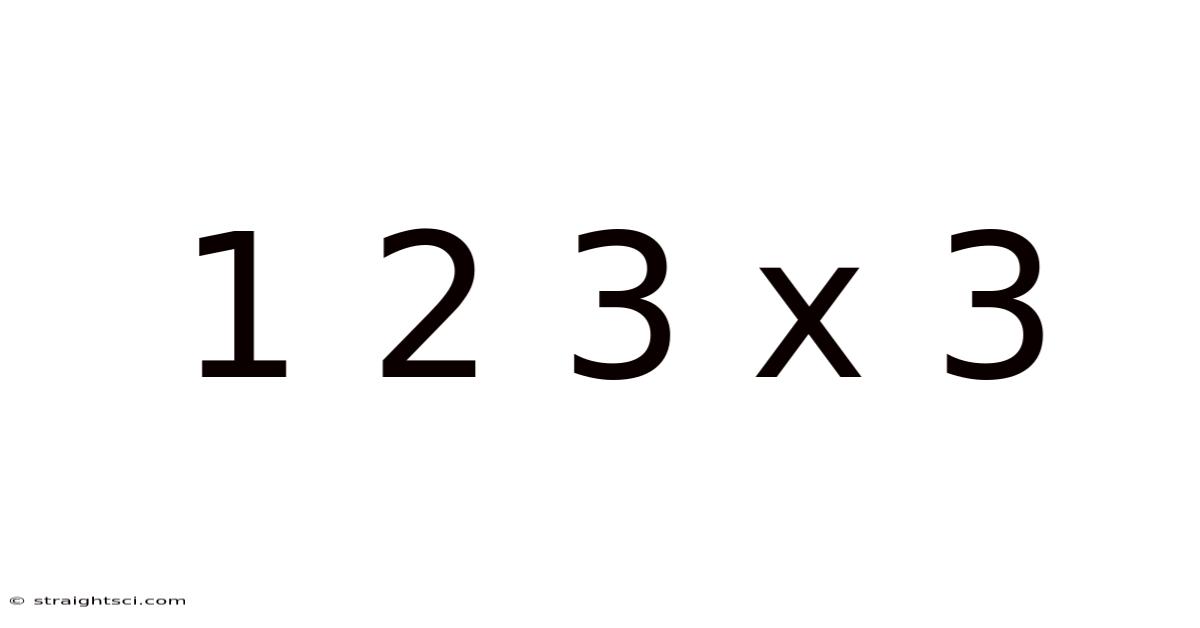
Table of Contents
Decoding 1 2 3 x 3: A Deep Dive into Multiplication, Patterns, and Beyond
Understanding multiplication is a cornerstone of mathematics, crucial for everything from basic arithmetic to advanced calculus. This article delves into the seemingly simple equation "1 2 3 x 3," exploring its fundamental components, uncovering hidden patterns, and expanding its application to broader mathematical concepts. We'll move beyond the basic calculation to discover the richness and significance of this seemingly simple expression.
Understanding the Basics: Multiplication and its Components
Before we dissect "1 2 3 x 3," let's refresh our understanding of multiplication itself. Multiplication is essentially repeated addition. When we say "3 x 3," we are essentially adding three threes together: 3 + 3 + 3 = 9. This fundamental concept underpins all multiplication operations.
In our target equation, "1 2 3 x 3," we encounter a slightly more complex scenario. The number "1 2 3" isn't a single digit but a three-digit number. Therefore, the equation is not simply "repeated addition" in the same straightforward way as "3 x 3". Instead, we're multiplying the number 123 by 3. This involves a more intricate process, typically learned through the method of long multiplication.
The Long Multiplication Method: Step-by-Step
The most common approach to solving "1 2 3 x 3" involves the long multiplication method. This methodical approach breaks down the multiplication into smaller, manageable steps. Let's walk through it:
Step 1: Multiply the Ones Digit
We begin by multiplying the ones digit of 123 (which is 3) by 3. 3 x 3 = 9. We write down the '9' in the ones column of our answer.
Step 2: Multiply the Tens Digit
Next, we multiply the tens digit of 123 (which is 2) by 3. 2 x 3 = 6. We write down the '6' in the tens column of our answer.
Step 3: Multiply the Hundreds Digit
Finally, we multiply the hundreds digit of 123 (which is 1) by 3. 1 x 3 = 3. We write down the '3' in the hundreds column of our answer.
Therefore, the solution to 123 x 3 is 369.
Beyond the Calculation: Exploring Patterns and Properties
While the long multiplication method provides a practical solution, it's crucial to appreciate the underlying mathematical principles at play. Analyzing "1 2 3 x 3" reveals some interesting patterns and properties:
-
Distributive Property: We can also solve this using the distributive property of multiplication over addition. We can rewrite 123 as 100 + 20 + 3. Then, the equation becomes: 3 x (100 + 20 + 3) = (3 x 100) + (3 x 20) + (3 x 3) = 300 + 60 + 9 = 369. This demonstrates the distributive property, where multiplying a sum by a number is the same as multiplying each addend by the number and then adding the products.
-
Place Value: The long multiplication method hinges on the concept of place value, where the position of a digit in a number determines its value (ones, tens, hundreds, etc.). Understanding place value is crucial for accurately performing multi-digit multiplication.
-
Number Properties: Exploring the factors and multiples involved can also be insightful. 123 is a composite number (a number with more than two factors), and 3 is a prime number (a number divisible only by 1 and itself). The product, 369, is also a composite number. Understanding the properties of these numbers enriches our understanding of the equation.
-
Patterns in Multiples: Looking at the multiples of 3, we observe a pattern: 3, 6, 9, 12, 15, and so on. The sum of the digits in each multiple is always divisible by 3 (3, 6, 9, 3, 6...). This pattern continues and applies to the result of 123 x 3; the sum of the digits in 369 (3+6+9 = 18) is also divisible by 3. This is an example of divisibility rules.
Expanding the Concept: Applications and Further Exploration
The seemingly simple equation, "1 2 3 x 3," serves as a springboard to explore many broader mathematical concepts.
-
Algebra: This can be generalized into algebraic expressions. For example, we could represent this as nx3, where n represents any three-digit number. Solving this would require using variables and applying the principles of algebraic manipulation.
-
Geometry: Multiplication is essential in geometrical calculations, such as finding the area of a rectangle (length x width) or the volume of a rectangular prism (length x width x height). Understanding multiplication allows us to solve problems related to shapes and spatial reasoning.
-
Real-World Applications: Multiplication is used extensively in various real-world scenarios. Calculating the total cost of multiple items, determining distances, or even converting units all involve multiplication. Understanding this equation provides a foundation for these practical applications.
-
Advanced Mathematics: The principles involved in this simple multiplication problem lay the groundwork for more complex mathematical concepts such as matrix multiplication, vector multiplication, and even more abstract mathematical operations encountered in higher levels of mathematics.
Frequently Asked Questions (FAQ)
Q: What is the quickest way to multiply 123 by 3?
A: The long multiplication method is systematic and reliable, but with practice, you can develop mental strategies for multiplication. For instance, you could break it down as (100 x 3) + (20 x 3) + (3 x 3), which is quickly solved mentally.
Q: Are there other methods to solve 123 x 3 besides long multiplication?
A: Yes, as mentioned above, the distributive property and mental math strategies are viable alternatives. Using a calculator is also a quick and efficient way to solve it.
Q: Why is understanding multiplication important?
A: Multiplication is a fundamental building block in mathematics and has numerous applications in everyday life and various fields of study. Proficiency in multiplication enhances problem-solving skills and lays the foundation for more advanced mathematical concepts.
Q: How can I improve my multiplication skills?
A: Practice is key! Consistent practice with various multiplication problems, using different methods, and working through word problems can significantly improve your understanding and speed.
Conclusion: The Significance of Simplicity
The equation "1 2 3 x 3" may appear elementary, but a thorough investigation reveals its significance as a fundamental building block in mathematics. From understanding the long multiplication method to applying the distributive property and exploring various patterns, this simple equation offers a gateway to a deeper appreciation of mathematical principles and their real-world applications. Mastering this fundamental concept paves the way for success in more advanced mathematical explorations and problem-solving in various fields. So, don't underestimate the power of this seemingly simple calculation – it's a microcosm of the beauty and elegance of mathematics itself.
Latest Posts
Latest Posts
-
What Is Shielded Arc Welding
Sep 03, 2025
-
Medical Term For Skin Scrape
Sep 03, 2025
-
The Hot Food Zone Is
Sep 03, 2025
-
Weight Of The Average Person
Sep 03, 2025
-
Bubble Skin Care For Kids
Sep 03, 2025
Related Post
Thank you for visiting our website which covers about 1 2 3 X 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.