1 1/6 As A Decimal
straightsci
Sep 09, 2025 · 5 min read
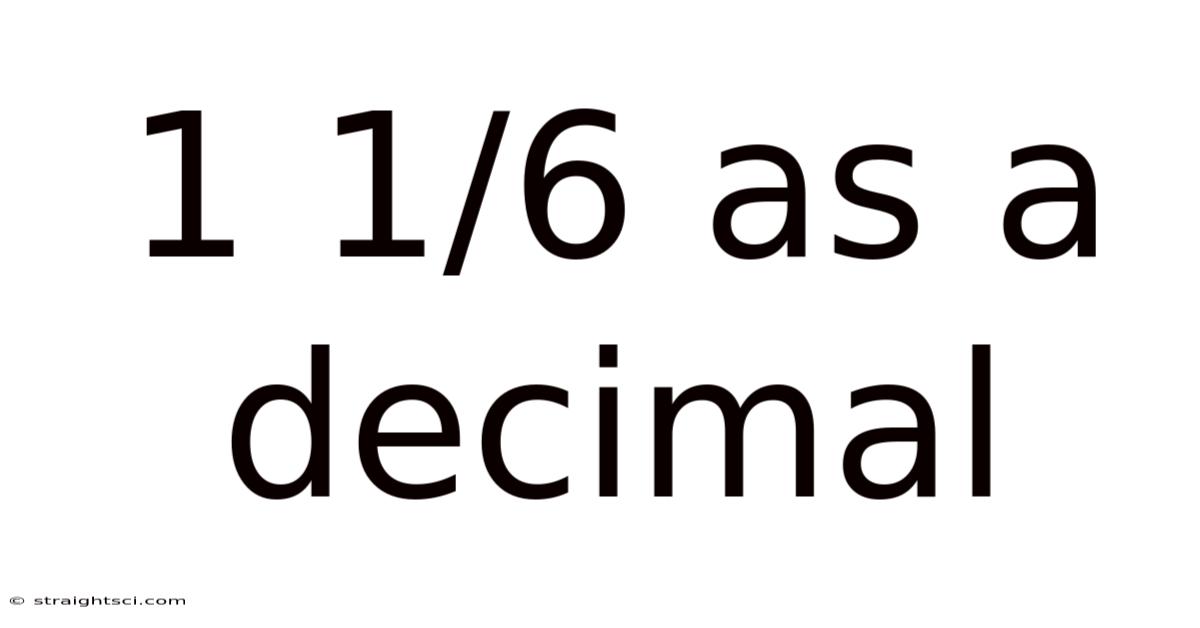
Table of Contents
Decoding 1 1/6 as a Decimal: A Comprehensive Guide
Converting fractions to decimals is a fundamental skill in mathematics, crucial for various applications from everyday calculations to advanced scientific computations. This article will delve into the process of converting the mixed fraction 1 1/6 into its decimal equivalent, providing a step-by-step guide suitable for learners of all levels. We'll explore different methods, explain the underlying principles, and address common misconceptions. By the end, you'll not only understand how to convert 1 1/6 to a decimal but also gain a broader understanding of fraction-to-decimal conversion.
Understanding Mixed Fractions and Decimals
Before we begin, let's clarify the terminology. A mixed fraction, like 1 1/6, consists of a whole number part (1) and a fractional part (1/6). A decimal, on the other hand, represents a number using a base-10 system, where digits to the right of the decimal point represent tenths, hundredths, thousandths, and so on. Converting a fraction to a decimal essentially means finding the equivalent decimal representation of that fraction.
Method 1: Converting the Fraction to a Decimal, Then Adding the Whole Number
This is arguably the most straightforward approach. We'll first convert the fractional part (1/6) to a decimal, and then add the whole number part (1).
-
Divide the numerator by the denominator: To convert 1/6 to a decimal, we divide the numerator (1) by the denominator (6): 1 ÷ 6 = 0.166666...
-
Notice the repeating decimal: The result is a repeating decimal, indicated by the ellipsis (...). The digit 6 repeats infinitely. We can represent this using a bar over the repeating digit: 0.16̅
-
Add the whole number: Now, we add the whole number part (1) to the decimal representation of the fraction: 1 + 0.16̅ = 1.16̅
Therefore, 1 1/6 as a decimal is 1.166666... or 1.16̅.
Method 2: Converting the Mixed Fraction to an Improper Fraction, Then to a Decimal
This method involves first converting the mixed fraction into an improper fraction, and then performing the division.
-
Convert to an improper fraction: To convert 1 1/6 to an improper fraction, we multiply the whole number (1) by the denominator (6), add the numerator (1), and keep the same denominator: (1 * 6 + 1) / 6 = 7/6
-
Divide the numerator by the denominator: Now, we divide the numerator (7) by the denominator (6): 7 ÷ 6 = 1.166666...
The result is the same as in Method 1: 1.16̅
Understanding Repeating Decimals
The appearance of a repeating decimal, like 0.16̅, highlights an important concept in mathematics. Not all fractions can be expressed as terminating decimals (decimals that end). Fractions whose denominators, in their simplest form, contain prime factors other than 2 and 5 will result in repeating decimals. Since the denominator of 1/6 (after simplification) is 6 (which has a prime factor of 3), we get a repeating decimal.
Rounding Repeating Decimals
In practical applications, we often need to round repeating decimals to a specific number of decimal places. For example, we might round 1.16̅ to:
- 1.17 (rounded to two decimal places)
- 1.167 (rounded to three decimal places)
The choice of rounding depends on the level of precision required. It's crucial to understand that rounding introduces a small degree of error, but it's often necessary for practical purposes.
Applications of Decimal Conversion
Converting fractions to decimals is essential in various real-world situations:
- Financial calculations: Calculating interest, discounts, and tax amounts often involves decimal numbers.
- Scientific measurements: Many scientific measurements use decimal notation for precision.
- Engineering and design: Precise calculations are critical in engineering and design projects.
- Computer programming: Decimal representation is fundamental in computer programming for numerical computations.
Further Exploration: Converting Other Fractions to Decimals
The methods described above can be applied to other fractions. The key is to understand the process of dividing the numerator by the denominator. Let's consider a few examples:
- 3/4: 3 ÷ 4 = 0.75 (a terminating decimal)
- 2/3: 2 ÷ 3 = 0.66666... or 0.6̅ (a repeating decimal)
- 5/8: 5 ÷ 8 = 0.625 (a terminating decimal)
Observe that fractions with denominators containing only factors of 2 and 5 result in terminating decimals, while those with other prime factors result in repeating decimals.
Frequently Asked Questions (FAQ)
Q1: Why is 1/6 a repeating decimal?
A1: Because the denominator 6 (which simplifies to 2 x 3) contains a prime factor (3) other than 2 or 5. Only fractions with denominators containing only 2 and/or 5 as prime factors will result in terminating decimals.
Q2: How many decimal places should I round to?
A2: The number of decimal places depends on the context and the required level of accuracy. In some cases, two or three decimal places might be sufficient, while in others, more precision might be needed.
Q3: Can all fractions be converted to decimals?
A3: Yes, all fractions can be converted to decimals, either terminating or repeating decimals.
Q4: What if the fraction is negative?
A4: If the fraction is negative (e.g., -1 1/6), simply perform the conversion as described above and add a negative sign to the result: -1.16̅
Q5: Are there other methods to convert fractions to decimals?
A5: While division is the most common method, other techniques might be used depending on the specific fraction and the level of mathematical sophistication. For instance, you can sometimes use equivalent fractions to simplify the conversion.
Conclusion: Mastering Fraction-to-Decimal Conversion
Converting fractions like 1 1/6 to decimals is a fundamental mathematical skill with broad applications. By understanding the underlying principles and practicing the different methods outlined in this article, you'll develop a solid understanding of this essential concept. Remember to pay attention to repeating decimals and the appropriate rounding techniques based on the context of your calculations. Mastering this skill will empower you to confidently tackle various mathematical and real-world problems. The ability to seamlessly transition between fractions and decimals opens doors to a deeper understanding of numerical representation and its practical applications across diverse fields.
Latest Posts
Latest Posts
-
Four Types Of Communication Skills
Sep 10, 2025
-
How To Remove Drawer Slides
Sep 10, 2025
-
I Miss You In Germany
Sep 10, 2025
-
Math Questions For 12th Graders
Sep 10, 2025
-
Internal Temperature Of Ground Pork
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about 1 1/6 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.