1 1/4 Divided By 2
straightsci
Sep 13, 2025 · 6 min read
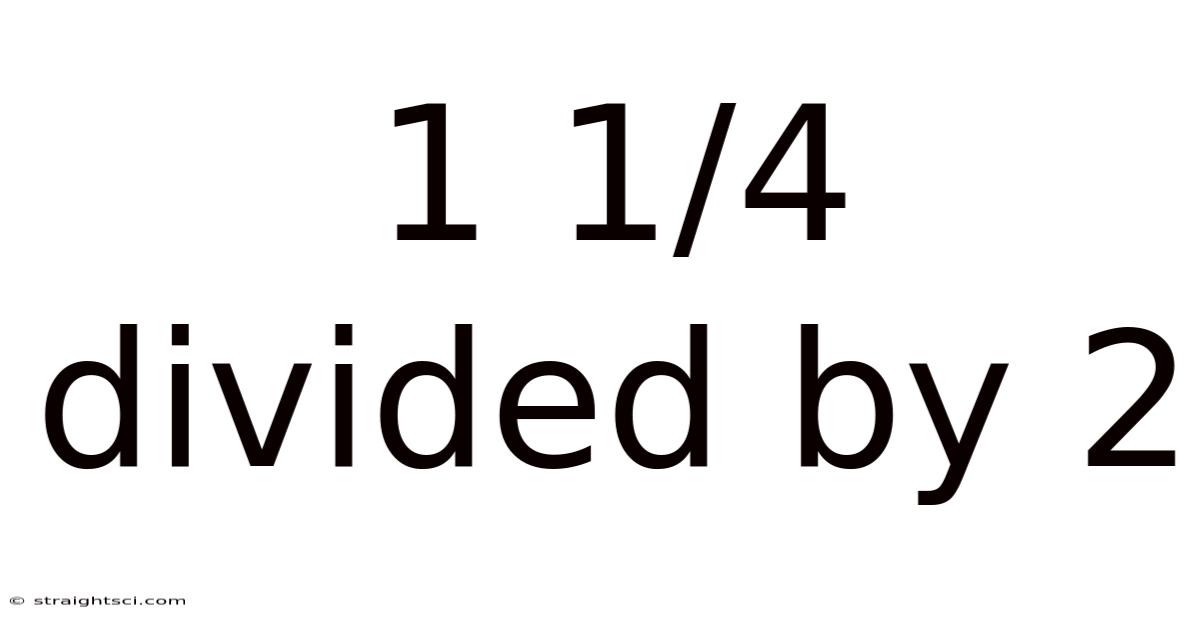
Table of Contents
Decoding the Division: A Deep Dive into 1 1/4 Divided by 2
This article explores the seemingly simple problem of dividing 1 1/4 by 2. While the calculation itself is straightforward, we’ll delve into multiple methods of solving it, emphasizing the underlying mathematical principles and providing a comprehensive understanding applicable to various similar problems. Understanding this seemingly basic calculation forms a cornerstone for more advanced mathematical concepts. This guide is designed for anyone looking to solidify their understanding of fractions and division, from elementary school students to adults brushing up on their math skills.
Understanding the Problem: 1 1/4 ÷ 2
The problem, 1 1/4 divided by 2, asks us to determine how many times the number 2 fits into 1 1/4. This involves a fundamental understanding of fractions and division. We'll cover various approaches to reach the solution, illustrating different methods and highlighting their advantages.
Method 1: Converting to Improper Fractions
This is arguably the most common and efficient method for dividing mixed numbers. The first step is to convert the mixed number, 1 1/4, into an improper fraction.
-
Step 1: Conversion to Improper Fraction: To convert 1 1/4 to an improper fraction, we multiply the whole number (1) by the denominator (4) and add the numerator (1). This sum (1*4 + 1 = 5) becomes the new numerator, while the denominator remains the same (4). Therefore, 1 1/4 is equivalent to 5/4.
-
Step 2: Division: Now our problem becomes 5/4 ÷ 2. Remember that dividing by a whole number is the same as multiplying by its reciprocal. The reciprocal of 2 is 1/2.
-
Step 3: Multiplication: So, we multiply 5/4 by 1/2: (5/4) * (1/2) = 5/8
-
Step 4: Simplification: The resulting fraction, 5/8, is already in its simplest form. Therefore, 1 1/4 divided by 2 equals 5/8.
Method 2: Decimal Conversion
Another approach involves converting both the mixed number and the divisor into decimals. This method can be particularly useful when using a calculator.
-
Step 1: Decimal Conversion: Convert 1 1/4 to a decimal. Since 1/4 is equal to 0.25, 1 1/4 is equal to 1.25.
-
Step 2: Division: Now, perform the decimal division: 1.25 ÷ 2 = 0.625
-
Step 3: Conversion (Optional): If needed, you can convert the decimal 0.625 back to a fraction. This involves placing the decimal over a power of 10 (in this case, 1000) and simplifying: 625/1000. Simplifying this fraction by dividing both the numerator and denominator by 125 gives us 5/8. Thus, the result is again 5/8.
Method 3: Visual Representation
While not as efficient for complex calculations, visualizing the problem can enhance understanding, particularly for beginners. Imagine a pizza cut into four slices. 1 1/4 pizzas represent one whole pizza and one quarter of another. We need to divide this total amount of pizza among two people. Each person will receive five slices, which represents 5/8 of a whole pizza.
Method 4: Long Division with Fractions
This method offers a more detailed, step-by-step approach to division involving fractions. Although it might seem more complex than the previous methods, it offers a deeper understanding of the underlying process.
-
Step 1: Rewrite the problem: Rewrite the problem as (1 + 1/4) / 2
-
Step 2: Distribute the division: We can distribute the division across the addition: (1/2) + (1/4)/2
-
Step 3: Simplify the second term: (1/4)/2 is the same as (1/4) * (1/2) = 1/8
-
Step 4: Combine the terms: The equation becomes (1/2) + (1/8). To add these fractions, we need a common denominator, which is 8.
-
Step 5: Find the common denominator: (1/2) is equivalent to 4/8.
-
Step 6: Add the fractions: 4/8 + 1/8 = 5/8
Therefore, the answer, once again, is 5/8.
The Importance of Understanding Different Methods
While all four methods yield the same correct answer (5/8), understanding each method provides a more profound grasp of the mathematical principles involved. The improper fraction method is generally the most efficient, while the decimal method is readily adaptable to calculators. The visual representation aids in intuitive understanding, and the long division method demonstrates the step-by-step application of fraction rules.
Extending the Understanding: More Complex Problems
The principles demonstrated here can be extended to more complex problems involving mixed numbers and division. The key is to consistently apply the rules of fraction manipulation: converting mixed numbers to improper fractions, finding common denominators for addition and subtraction, and using reciprocals for division.
For example, let's consider a slightly more challenging problem: 2 3/5 ÷ 1 1/2.
- Convert to improper fractions: 2 3/5 becomes 13/5, and 1 1/2 becomes 3/2.
- Perform the division: (13/5) ÷ (3/2) = (13/5) * (2/3) = 26/15
- Simplify (if possible): 26/15 can be expressed as a mixed number: 1 11/15
Therefore, 2 3/5 divided by 1 1/2 equals 1 11/15.
Frequently Asked Questions (FAQ)
-
Q: Can I use a calculator to solve this problem? A: Yes, you can use a calculator to solve this problem, particularly using the decimal conversion method. However, understanding the underlying principles remains crucial for broader mathematical comprehension.
-
Q: Why is it important to convert mixed numbers to improper fractions before dividing? A: Converting to improper fractions simplifies the division process, eliminating the need for separate operations with the whole number and fractional parts.
-
Q: What if the divisor is a fraction? A: The principle remains the same; you would multiply by the reciprocal of the fractional divisor.
-
Q: Are there any other ways to solve this type of problem? A: While the methods discussed are the most common and efficient, variations exist depending on individual approaches and mathematical comfort levels. The core principles, however, remain consistent.
Conclusion: Mastering Fraction Division
Dividing 1 1/4 by 2, while appearing simple, provides a valuable opportunity to reinforce fundamental concepts in fraction arithmetic and division. Mastering these techniques is critical for building a strong foundation in mathematics. By understanding and applying the various methods described, you can confidently tackle more complex fraction problems and further enhance your mathematical skills. Remember that consistent practice and exploration of different approaches are key to solidifying your understanding. The seemingly simple problem of 1 1/4 divided by 2 opens the door to a deeper appreciation of the elegance and power of mathematical reasoning. Keep practicing, and you'll soon find that these calculations become second nature.
Latest Posts
Latest Posts
-
How Far Does Bullet Travel
Sep 13, 2025
-
What Is The Turgor Pressure
Sep 13, 2025
-
Where Is The Femur Located
Sep 13, 2025
-
Formula For Copper I Oxide
Sep 13, 2025
-
Newtons Law Of Gravitation Formula
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about 1 1/4 Divided By 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.