1 1/10 As A Percent
straightsci
Sep 20, 2025 · 5 min read
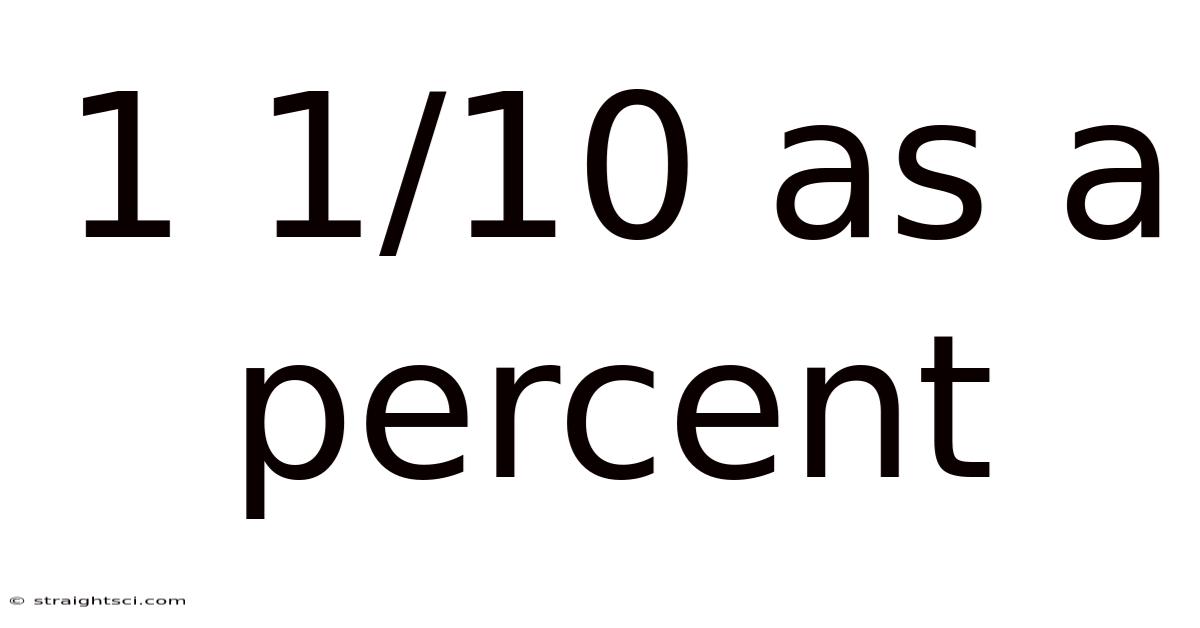
Table of Contents
Understanding 1 1/10 as a Percent: A Comprehensive Guide
Converting fractions to percentages is a fundamental skill in mathematics with applications across various fields, from finance and statistics to everyday budgeting and cooking. This article will delve into the process of converting the mixed number 1 1/10 into a percentage, explaining the steps involved in detail, exploring the underlying concepts, and providing practical examples to solidify your understanding. This guide is designed for anyone needing to grasp this essential conversion, from students refreshing their math skills to professionals needing a quick refresher.
Understanding Percentages
Before diving into the conversion, let's revisit the core concept of percentages. A percentage is simply a fraction where the denominator is 100. It represents a proportion or a part of a whole expressed as a number out of 100. The symbol "%" signifies "per cent," meaning "out of one hundred." For example, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or the decimal 0.5.
Converting 1 1/10 to an Improper Fraction
The first step in converting 1 1/10 to a percentage involves transforming the mixed number into an improper fraction. A mixed number combines a whole number and a fraction. In this case, we have 1 (the whole number) and 1/10 (the fraction). To convert it to an improper fraction, we multiply the whole number by the denominator of the fraction and add the numerator. This result then becomes the new numerator, while the denominator remains the same.
Here's how it works:
- Multiply the whole number by the denominator: 1 * 10 = 10
- Add the numerator: 10 + 1 = 11
- Keep the same denominator: 10
Therefore, 1 1/10 as an improper fraction is 11/10.
Converting the Improper Fraction to a Decimal
The next step is to convert the improper fraction 11/10 into a decimal. To do this, we simply divide the numerator (11) by the denominator (10).
11 ÷ 10 = 1.1
So, 11/10 is equivalent to 1.1 as a decimal.
Converting the Decimal to a Percentage
Finally, we convert the decimal 1.1 into a percentage. To do this, we multiply the decimal by 100 and add the percentage symbol (%).
1.1 * 100 = 110
Therefore, 1.1 as a decimal is equal to 110%.
Putting it All Together: The Complete Conversion
Let's summarize the entire process of converting 1 1/10 to a percentage:
- Mixed Number to Improper Fraction: 1 1/10 = 11/10
- Improper Fraction to Decimal: 11/10 = 1.1
- Decimal to Percentage: 1.1 * 100% = 110%
Therefore, 1 1/10 is equivalent to 110%.
Why is it More Than 100%?
It's important to understand that a percentage greater than 100% signifies a value exceeding the original whole. In this case, 110% indicates that the quantity is 10% more than the initial whole. This is perfectly valid and commonly used in various contexts, such as expressing growth, increases, or exceeding a target. For instance, if a company's sales increased from 100 units to 110 units, the increase would be represented as a 110% of the original sales.
Practical Applications and Real-World Examples
Understanding the conversion of fractions to percentages has numerous practical applications. Here are a few examples:
- Finance: Calculating interest rates, profit margins, and percentage changes in investment values. For example, if you invest $100 and earn $10 profit, your return on investment is 110% of your initial investment.
- Statistics: Expressing data as proportions or probabilities. For example, if 11 out of 10 people in a survey respond positively, this can be represented as 110%.
- Everyday Life: Calculating discounts, tips, or tax amounts. Imagine a 10% increase in the price of a product initially costing $100. The final cost would be 110% of $100, or $110.
- Science: Representing experimental results or data analysis, often used in relative growth rate calculations.
Advanced Concepts and Related Conversions
While we've focused on 1 1/10, the principles discussed are applicable to converting any mixed number or fraction into a percentage. You can follow the same three-step process: converting to an improper fraction, then to a decimal, and finally to a percentage. This fundamental understanding allows you to tackle more complex percentage calculations involving larger numbers and different fraction types.
Furthermore, understanding the relationship between fractions, decimals, and percentages allows for easy conversions in the other direction. For instance, converting a percentage to a fraction or a decimal requires reversing the process outlined above: divide the percentage by 100 to get the decimal, and then convert the decimal to a fraction.
Frequently Asked Questions (FAQs)
Q1: Can a percentage be greater than 100%?
Yes, absolutely. A percentage greater than 100% represents a value that exceeds the original whole or baseline.
Q2: What if I have a fraction with a larger numerator than denominator?
This is an improper fraction. You convert it to a decimal (numerator divided by denominator) and then to a percentage (decimal multiplied by 100).
Q3: How do I convert a decimal directly to a percentage?
Multiply the decimal by 100 and add the percent sign (%).
Q4: What are some common mistakes people make when converting fractions to percentages?
Common mistakes include incorrectly converting mixed numbers to improper fractions, misplacing the decimal point during division, and forgetting to multiply by 100 when converting from a decimal to a percentage.
Q5: Are there any online tools or calculators available to assist with these conversions?
While this article aims to provide a thorough understanding of the process, many online calculators are available that can perform these conversions automatically. However, grasping the underlying principles remains crucial for understanding the mathematics involved.
Conclusion
Converting 1 1/10 to a percentage, resulting in 110%, is a straightforward process involving three key steps: converting the mixed number to an improper fraction, converting the improper fraction to a decimal, and finally, converting the decimal to a percentage. This process is not just limited to this specific example; it’s a fundamental skill applicable to a broad range of mathematical problems and real-world applications. Understanding the underlying principles, as detailed in this guide, enables you to confidently tackle similar conversions and reinforces your grasp of fundamental mathematical concepts. The ability to seamlessly navigate between fractions, decimals, and percentages is a valuable asset in various fields, ensuring effective problem-solving and data interpretation.
Latest Posts
Latest Posts
-
1 65 Metres In Feet
Sep 20, 2025
-
Example Of A Static Stretch
Sep 20, 2025
-
2 2k Ohm Resistor Color Code
Sep 20, 2025
-
11 Degrees Fahrenheit To Celsius
Sep 20, 2025
-
How To Food Cost Formula
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about 1 1/10 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.